Com treballar les ISOMETRIAS
En aquest taller veurem maneres diferents d'utilitzar les isometries que hem vist en aquest llibre:
- De forma gràfica, utilitzant la barra d'eines.
- De forma escrita, útil si volem fer animacions.
- Animacions de les transformacions per barres lliscants.
- Ús de seqüències per a crear les tessel·lacions i rotacions.
- I també podem jugar amb la transparència de la figura o imatge al donar-li moviment.
Properament miraré de crear diferents vídeos amb petites explicacions del que veurem durant aquest taller.
PRIMER DE TOT
Us escric aproximadament el què anirem fent, primer de tot us heu de descarregar aquesta plantilla de GeoGebra, la qual utilitzarem per veure els primers passos d’animació de les diferents transformacions isomètriques; translació, simetria i gir.
Per descarregar el document heu d’anar:
- als tres botons de dalt a la dreta i obrir el desplegable
- seleccionar detalls
- veureu una casella que posa descàrrega
- Clicar que “Estic d'acord amb els termes de la Llicència d'ús no-commercial de GeoGebra.”
ISOMETRIES
Amb aquest document pretenc treballar les tres transformacions isomètriques principals; translació, simetria i gir.
TRANSLACIÓ
Treballarem diferents maneres de fer la translació.
, en aquest cas mov i la definirem amb valors entre 0 i 1 amb un increment de 0,01 perquè no vagi a salts.
Escriurem aquesta definició:
Translació(pol1, mov v)
I si variem el valor de la barra lliscant, veurem que el quadrat es desplaça fins a la posició que volem, com podeu observar tampoc es traslladen els vèrtexs del quadrat.
També ho podem fer amb el polígon irregular i veurem que en aquest cas si que es desplacen els vèrtexs.
Translació(pol2, mov v)
Si mirem com l'ha definit, veurem que posa: Polígon(B'_{1}, C'_{1}, D'_{1}, F'_{1}, J'_{1}, K'_{1}) si us hi fixeu són tot de vèrtexs nous que s'han creat amb aquesta translació. I cada punt, per exemple F'_{1}=Translació(F, Vector(mov v))
- GRÀFICAMENT. Utilitzant l’eina translació
que trobareu al menú de transformacions utilitzant la tecla, haurem de clicar sobre l’objecte, en aquest cas el quadrat superior on posa TRANSLACIÓ i després clicar sobre el vector 
que determina la translació, u. - ESCRIVINT A LA BARRA D'ENTRADA. Si volem descobrir l'escriptura de les ordres només cal anar a la definició que ens dona la finestra de propietats de tots els objectes que usem. La translació es defineix així:
- Usant una VARIABLE que multipliqui el vector. La longitud del vector la podem variar utilitzant un valor que el multipliqui, si el vector que utilitzem ens indica el recorregut complet de la translació haurem d'utilitzar una variable que vagi entre 0 i 1.
, en aquest cas mov i la definirem amb valors entre 0 i 1 amb un increment de 0,01 perquè no vagi a salts.
Escriurem aquesta definició:
Translació(pol1, mov v)
I si variem el valor de la barra lliscant, veurem que el quadrat es desplaça fins a la posició que volem, com podeu observar tampoc es traslladen els vèrtexs del quadrat.
També ho podem fer amb el polígon irregular i veurem que en aquest cas si que es desplacen els vèrtexs.
Translació(pol2, mov v)
Si mirem com l'ha definit, veurem que posa: Polígon(B'_{1}, C'_{1}, D'_{1}, F'_{1}, J'_{1}, K'_{1}) si us hi fixeu són tot de vèrtexs nous que s'han creat amb aquesta translació. I cada punt, per exemple F'_{1}=Translació(F, Vector(mov v))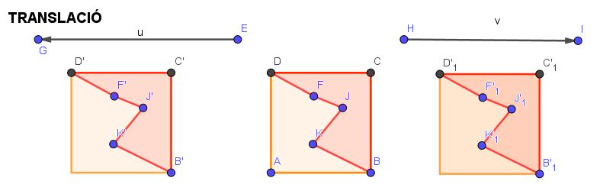 
SIMETRIA axial
També veurem diferents maneres de fer la simetria axial.
- GRÀFICAMENT. Per fer una simetria necessitem un eix de simetria (segment, semirecta o recta) i utilitzarem l'eina simetria
, clicarem sobre l'objecte a fer la simetria i després a l'eix de simetria. - ESCRIVINT A LA BARRA D'ENTRADA. Si continuem descobrint l'escriptura de les diferents transformacions, veurem que s'escriu així:
- ANIMEM LA SIMETRIA. Si pensem una simetria com si la figura fos un full de paper i el que fem és girar-lo com si l'eix fos on s'uneixen totes les pàgines podríem entendre que la figura ens quedi girada.
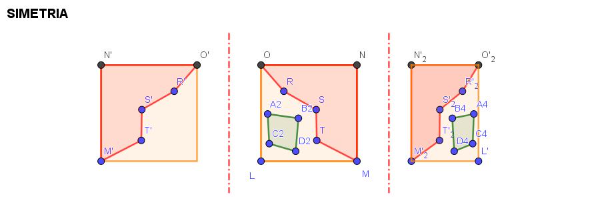
- UTILITZATN EL FULL DE CÀLCUL. Quan hem de fer per escrit elements molt repetitius el que podem fer és usar el full de càlcul, ja veureu que us farà la vida més fàcil. Per fer-ho farem un nou quadrilàter a partir de quatre punts.
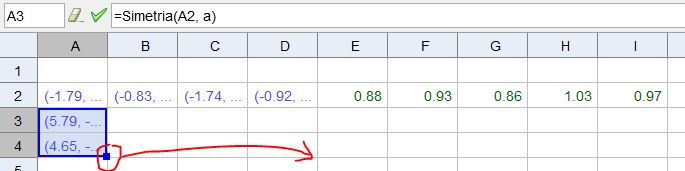
Per crear el polígon només cal seleccionar la casella E2 i arrossegar-la cap avall, dues posicions.
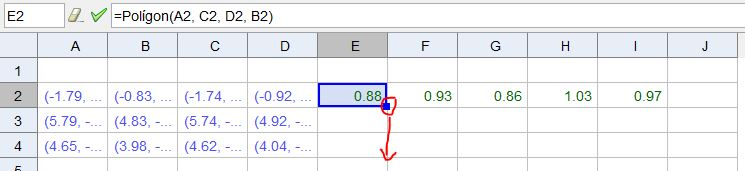
Ja tenim els polígons creats i ara només cal seleccionar la fila 3 i ocultar tots els elements, clicant sobre el número 3 davant de la fila i usant el botó dret.
I ja hem vist les diferents maneres de fer les simetries.
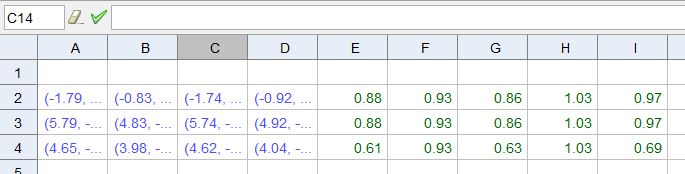
GIR o ROTACIÓ
En aquesta transformació, el gir 
veurem l'ús d'imatges, de la transparència i de les seqüències per fer els diferents girs.
veurem l'ús d'imatges, de la transparència i de les seqüències per fer els diferents girs.
- GRÀFICAMENT. Per fer un gir necessitem un centre de gir o punt de rotació, un cop el tenim seleccionem l'ordre rotació al voltant d'un punt
, clicarem sobre l'objecte, el centre de gir (c_1) i ens sortirà una casella emergent on haurem d'escriure l'angle de gir (90º) i indicar el seu sentit, horari o antihorari. - ESCRIVINT A LA BARRA D'ENTRADA. Mirem l'escriptura del gir que acabem de fer:
- ANIMEM EL GIR. El gir és molt fàcil animar-lo, ja que només cal crear una barra lliscant definida com a angle i situar-lo allà on hem posat 90º.
- ANIMEM la ROTACIÓ i la TRANSPARÈNCIA. Ara el què farem és girar el quadrat utilitzant un vèrtex i crear 4 quadrats sense deixar espais entre ells, un gir d'ordre 4, girant cada quadrat 90º. Com que hem de fer més girs, el què farem serà usar una nova barra lliscant gir que definirem de 0 a 4 amb intervals de 0.01. I escriurem:
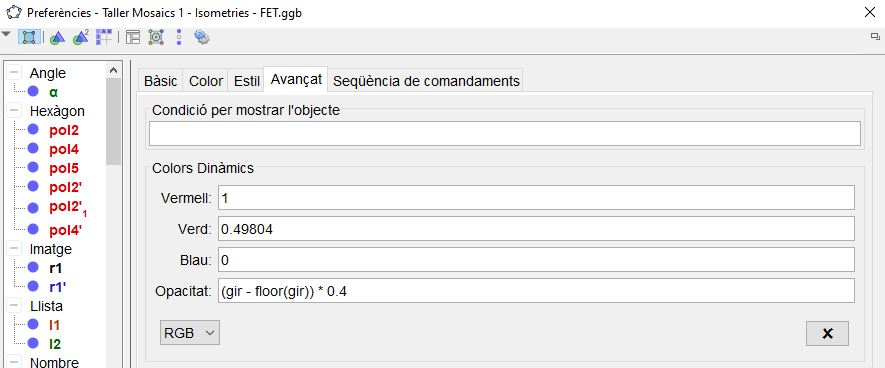
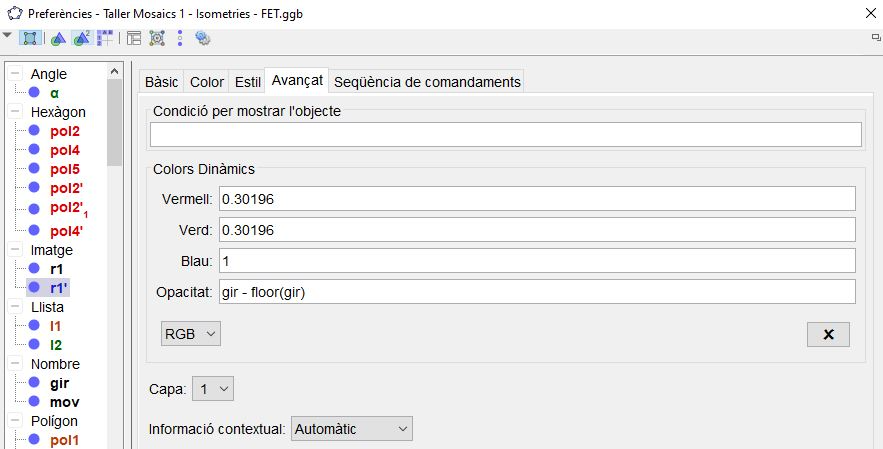
(gir - floor(gir)) * 0.4
Fixeu-vos que automàticament se'ns han omplert els valors que defineixen el color (vermell, verd i blau), en funció del color que era el quadrat, ja no el podrem modificar pels mètodes convencionals.
L'OPACITAT és un valor que va de 0 (transparent) a 1 (opac), per tant, ha d'anar de 0 a 1.
L'expressió floor(gir) escapça el valor de la variable gir i ens dona només l'enter, en conseqüència, quan gir val més de 1, si fem gir - floor(gir) estem agafant només els decimals de gir (menors a 1). El número 0.4 del final defineix la transparència final que voldrem aconseguir quan arribi a 1.
Ara hem de fer un altre gir que deixi fixa un quadrat en cada posició de 90º, a cada valor enter de gir, per fer-ho farem una seqüència.
Què és una seqüència, és una repetició d'una ordre repetitiva la qual es modifica a partir d'una variable, és aquest cas, el primer gir serà de 90º, el segon de 2x90º, 3x90º, etc.. per tant, és fàcil d'utilitzar. L'ordre es defineix així: Seqüència( , , , , ).
Expressió serà l'ordre de rotació, on el número que multiplica el gir serà la variable (i)
Variable, serà la lletra que usarem dins l'expressió, en aquest cas i.
Valor inicial, si volem que faci el primer quadrat sense girar hauria de començar a zero, sinó en 1.
Valor final, el nombre total de girs que volem, coincidiria amb l'ordre de gir-1.
Increment, com vols que variï aquesta variable, si és d'1 en 1, no caldrà posar res.
Haurem d'escriure:
Seqüència(Rotació(pol6, i (-90°), Z), i, 1, gir)
L'expressió és igual que l'anterior, però posant la variable i en el lloc del gir i a darrera definim entre comes la variable que comença a 1 i acaba amb el valor de gir, d'aquesta manera els quadrats aniran apareixent a mesura que la variable gir va augmentant... i l'altre quadrat va girant.
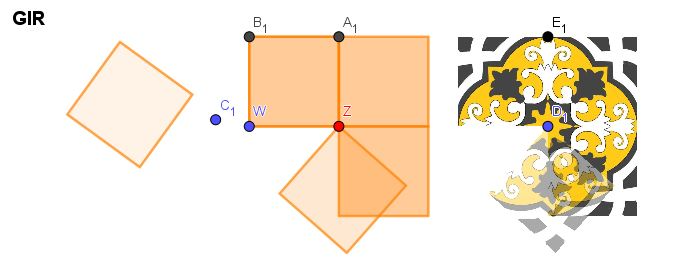
En aquesta imatge es pot veure el resultat, si us hi fixeu també ho podem fer amb la imatge que tenim al costat i funciona de la mateixa manera...
- ANIMACIÓ i ROTACIÓ d'una IMATGE utilitzant la TRANSPARÈNCIA. Per fer-ho usarem aquestes expressions, que són idèntiques de les del quadrat, però amb les dades de la imatge (r1) i el vèrtex que la defineix D_1.
