Sucesiones y Series
Sucesiones
Series
Ahora que ya conoces las sucesiones, debemos aprender como sumarlas. Cuando sumamos una sucesión infinita esta toma el nombre de serie, (pareciera que fuese otro nombre para las sucesiones, pero en realidad es una suma).
Ejemplo: Números impares Sucesión: {1, 3, 5, 7, ...} Serie: 1 + 3 + 5 + 7 + ...
Series infinitas
Cuando tenemos una secuencia infinita de valores que siguen una regla (en este caso, cada termino es la mitad del anterior) y los sumamos todos:
1/2 + 1/4 + 1/8 + 1/16, + ... = S
obtenemos una serie infinita.Notación
A menudo se usa la notación Sigma para series infinitas. El ejemplo anterior se vería así:
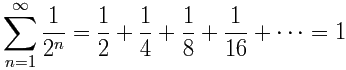
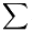Este símbolo (llamado sigma) significa "sumar".
Convergencia
Sumemos los términos un a la vez. Cuando la "suma hasta un cierto valor" se acerca a un valor finito, se dice que la serie es "convergente":
Nuestro primer ejemplo:
1/2 + 1/4 + 1/8 + 1/16 + ...
Va sumando así:
Las sumas se dirigen hacia un valor (1 en este caso), por lo que esta serie es convergente.
| Término | Suma hasta cierto valor |
| 1/2 | 0.5 |
| 1/4 | 0.75 |
| 1/8 | 0.875 |
| 1/16 | 0.9375 |
| 1/32 | 0.96875 |
| ... | ... |