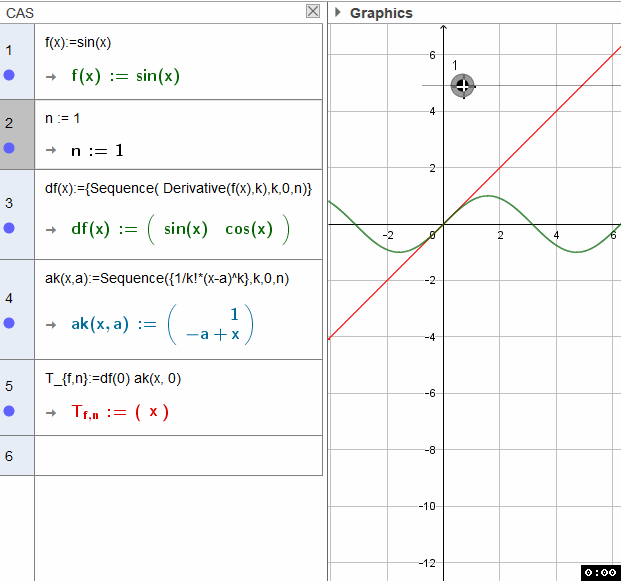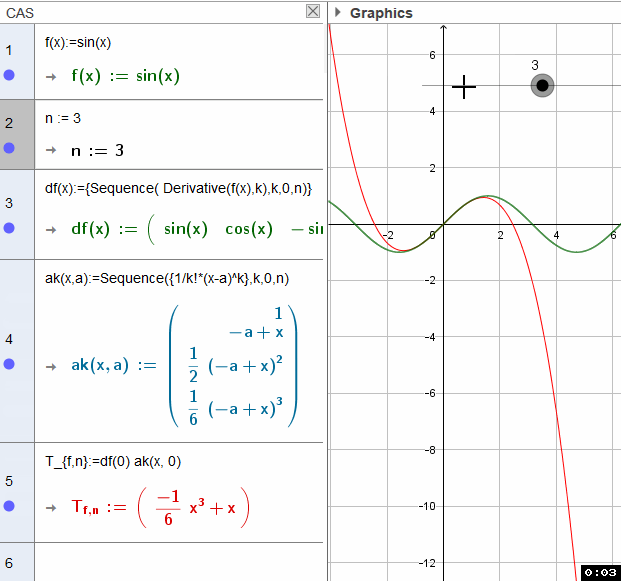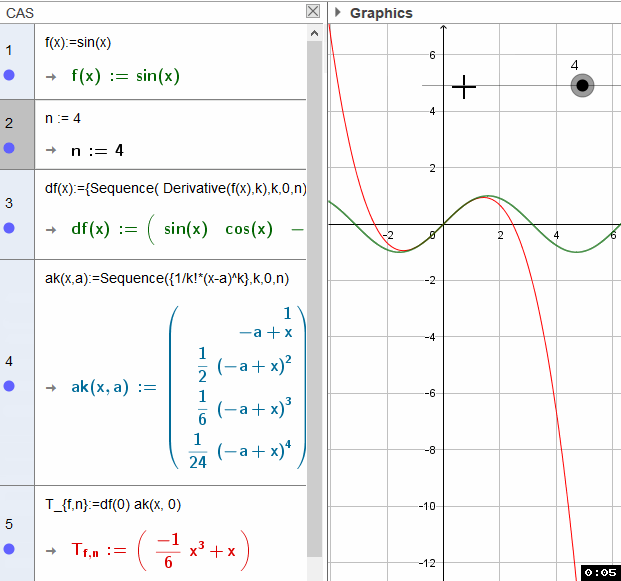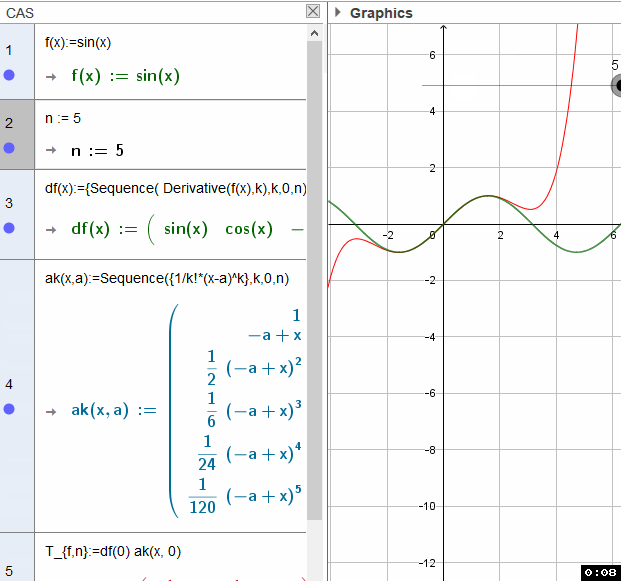
Taylorpolynom (selbst) entwicklen (Taylor Polynomial)
Die Auswertung der Liste der Ableitungen ist etwas tricky - ich stelle mal mehrere Möglichkeiten vor - solche (nicht explizit dokumentierte) Funktionalitäten haben die Eigenart im Rahmen der Produktpflege verloren zu gehen:
dfx=Sequence(Derivative(f, k), k, 0, n)
{Zip(F(x(a)),F,dfx)}
{Sequence(dfx(k, a), k, 1, n + 1)}
{Zip(dfx(i, a), i, Sequence(k, k, 1, n + 1))}
{Sequence(Iteration(Element(dfx, k), a, 1), k, 1, n + 1)}
im CAS sind Listen-Argument-Funktionen möglich
DF(x):={Sequence(Derivative(f, k), k, 0, n)}
df:DF(a)
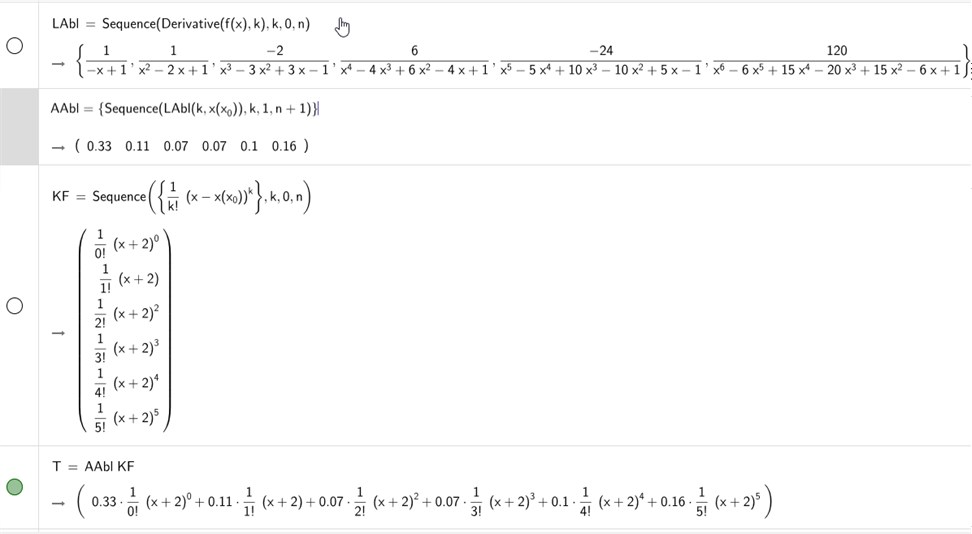
Ableitungen dfx an der Stelle x(x_0) berechnen und in eine Zeilenmatrix stellen dfa.
Eine Spaltenmatrix kx mit den Faktoren 1/k! (x-x(x_0)) erstellen.
Summe: beide multiplizieren (zeile*spalte)
CAS List Argument Function