Parameter-Kurve kubische Splines
SplineParameterCurve_Matrix Alg
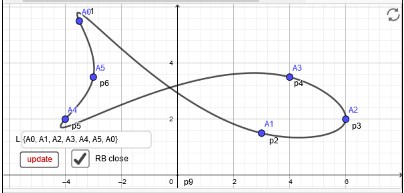
Umsetzung für CAS von https://www.geogebra.org/material/show/id/q83UFJsT
z.Z. keine Eingabe über Inputbox möglich - select A0..A9 by slider - RB close {A0...Ap_nA0}!
Es werden voll besetzte Polynome verwendet
wo bei t beginnend bei 0 in die Abschnitte
eingeteilt wird (also die Entfernung der Punkte). Setze die Pfadlänge des Splines =1, t0=0 , to=t1...tn=1.
Neue Punkte in Liste L (5) eintragen - [update] nach Hinzufügen oder Entfernen von Punkten/Stützstellen.
Wenn die Curve geschlossen werden soll machen sich die Randbedingungen [RB close] besser
(RB) s6=if(RB,{p1(0)-p'n(to(n))=0,p''n(to(n))-p''1(0)=0} , {p'1(0)=0,p'n(to(n))=0})
gleiche Steigung und Krümmung beim Übergang 1. Polynom zu n.tes Polynom - Krümmung 1.Stützpunkt(t=0) im 1. Polynom und n+1.ter Stützpunkt (t=to(n) im n.ten Polynom=0!
Das LGS lege ich als Matrix S an, je 4 Spalten enthalten die Koeffizienten der Splinepolynome (
erste 4 Spalten ~ erstes Polynom, ... n.te 4 Spalten ~ n.tes Polynom.
aij =,
| Stützstellen | x(t) | (t0=0,X(1) | (t1,X(2) | (t2,X(3) | (t3,X(4) | (t4=1,X(5) |
| z.B. n=4: | y(t) | (t0=0,Y(1) | (t1,Y(2) | (t2,Y(3) | (t3,Y(4) | (t4=1,Y(5) |
| s1= | {p1(0)} {pn(1)} | = X(1) , Y(1) = X(n+1),Y(n+1) | s2= | {p1(t1)} {p2(t1)} {p3(t2)} | = X(2), Y(2) = X(3), Y(3) = X(4), Y(4) | s3= | {p2(t2)} {p3(t3)} {p4(t3)} | = X(2), Y(2) = X(3), Y(3) = X(4), Y(4) |
Geschlossener Spline (Punktliste Anfang=Ende)