Carretillas de Penrose
Esta actividad pertenece al libro de GeoGebra La fábrica de teselados.
El azulejo fundamental puede ser bastante complejo. La siguiente figura se conoce como "carretilla de Penrose". Es un poliamante, es decir, una figura formada por triángulos equiláteros. En el caso de los "diamantes" (como el del palo de la baraja francesa) son 2 triángulos. En el caso de la carretilla, son 18, como muestra la siguiente imagen.
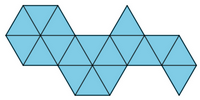
La carretilla compuesta por 18 triángulos equiláteros que hemos tomado como base de nuestro azulejo es:
k = sqrt(3)/10
p = {Polígono((0, 0), (0, 0.2), (-k, 0.3), (-k, 0.5), (0, 0.6), (-k, 0.7), (-2k, 0.6), (-2k, 0.4), (-3k, 0.3), (-2k, 0.2), (-2k, 0), (-3k, -0.1), (-3k, -0.3), (-2k, -0.4), (-k, -0.3), (-k, -0.1))}
Ahora rotamos y reflejamos esa carretilla 12 veces hasta componer el azulejo fundamental, que tiene un perfil que podríamos describir vagamente como "un hexágono regular con entrantes y salientes". Solo se necesitan tres colores para colorearlo debidamente.
Estas son las variaciones que hemos realizado en la construcción plantilla:
númeroListas = 3
lista1 = {p, Rota(p, π, (-3k, 0.3)), Rota(Refleja(p, EjeY), -2π/3, (k, -0.3)), Rota(Rota(Rota(Refleja(p, EjeY), -2π/3, (k, -0.3)), -π/3, (6k, -0.6)), -2π/3)}
lista2 = {Rota(p, 2π/3), Rota(Rota(p, π, (-3k, 0.3)), 2π/3), Rota(Rota(Refleja(p, EjeY), -2π/3, (k, -0.3)), -π/3, (6k, -0.6)), Rota(Rota(Refleja(p, EjeY), -2π/3, (k, -0.3)), 2π/3)}
lista3 = {Rota(p, -2π/3), Rota(Rota(p, π, (-3 k, 0.3)), -2π/3), Rota(Rota(Rota(Refleja(p, EjeY), -2π/3, (k, -0.3)), (-π)/3, (6k, -0.6)), 2π/3), Rota(Rota(Refleja(p, EjeY), -2π/3, (k, -0.3)), -2π/3)}
u = (12k, 0)
v = (-6k, 1.8)
Colores elegidos por defecto:
paleta = {{51, 235, 255}, {0, 51, 204}, {130, 130, 0}}
Si observas que la velocidad de ejecución se ralentiza después de activar algunas casillas para elegir otras opciones, prueba a recargar esta página y elegir las casillas deseadas antes de iniciar la ejecución. Si tienes instalado GeoGebra, también puedes descargar el archivo GGB.
Si sustituimos la vista gráfica por la vista estándar 3D (configurada con perspectiva a distancia 500), el teselado se mostrará como un pavimento que se extiende hasta el horizonte.
Autor de la actividad y construcciones GeoGebra: Rafael Losada.