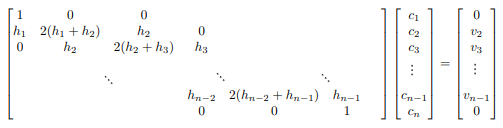Teorema de unicidad de la spline cúbica natural
Conceptos previos
Antes de enunciar y demostrar el Teorema para la Formula del Error en la Interpolación Polinomial es necesario un repaso con herramientas auxiliares que usaremos más adelante. 1. Matriz diagonal estrictamente dominante. Se dice que una matriz cuadrada ( x ) es diagonal estrictamente dominante o que es estrictamente dominante por filas, si y sólo si
>,
es decir, una matriz es estrictamente dominante diagonalmente cuando los elementos de la diagonal principal con mayores en valor absoluto, que la suma de los valores absolutos que los demás elementos de la fila correspondiente.
2. Teorema. Toda matriz diagonal estrictamente dominante es inversible. 3. Teorema. Para una matriz de x , las siguientes afirmaciones son equivalentes. es inversible. El sistema homogéneo tiene solo la solución trivial . El sistema de ecuaciones tiene una solución para cada matriz x , .Teorema de unicidad de la spline cúbica natural
Sean parejas de puntos tales que <<<. Entonces existe una y sólo una spline cúbica natural que satisface para . Demostración: Los trazadores cúbicos para , que componen a la spline cúbica natural están determinados por las valores de y . Ahora, por la construcción de los trazadores cúbicos, sabemos que para ,
y para ,la única variable resulta ser para ya que y dependen de ésta y los demás valores ya son conocidos. Entonces, si los valores de son constantes implica que la spline cúbica natural que interpola las parejas de puntos es única. Si es una spline cúbica natural sabemos que y que los valores de para están determinados por la matriz