Experimentación y formulación de una conjetura
El enunciado del problema es el siguiente:
¿Cuál es el mínimo número de cámaras que se necesitan para vigilar una galería de arte?
Consideramos la planta de la galería de arte como un polígono simple del plano formado por n lados, es decir, la galería de arte está cerrada por paredes (segmentos en el plano) que no se intersecan entre sí. Las cámaras de vigilancia permanecen en una situación fija dentro de la galería, aunque pueden controlar cualquier punto a su alrededor girando 360º . Los lugares vigilados son aquellos puntos del interior de la galería que se pueden conectar mediante un segmento con el punto en el que está situada la cámara. A lo largo del texto, utilizaremos el término sala para referirnos a la planta poligonal de la galería.Para resolver el problema con GeoGebra los alumnos podrían empezar experimentando con salas convexas, desarrollando el siguiente applet
Applet 1
Desde el punto cámara se traza un segmento que gira en torno a dicho punto ; el otro extremo del segmento, que llamamos PuntoPared, se sitúa en las paredes de la sala. Se trata de imitar la emisión de un rayo láser. Para ello, hemos implementado en dicho applet un script[1], realizado en GGBScript, un lenguaje de scripting propio de GeoGebra, que ejecuta el algoritmo encargado de realizar las siguientes acciones:
- Permitir colocar la cámara tanto en el interior de la sala como en sus paredes, pero nunca en el exterior.
- Mantener siempre el segmento en el interior de la sala.
- No permitir que el segmento atraviese ninguna pared de la sala.
- Facilitar la animación del giro del rayo, de a , en torno a la cámara.
- Posibilitar que los vértices de la sala puedan moverse libremente.
Desplazando el deslizador o pulsando el botón play se activa la animación. Además de utilizar el deslizador, los estudiantes pueden experimentar moviendo los diferentes vértices. Siempre que la sala se mantenga convexa percibirán que la colocación de una única cámara es suficiente para vigilarla en su totalidad, independientemente del número de paredes y de que sea regular o irregular.
De esta experimentación los alumnos pueden generar una primera conjetura:
Cualquier sala poligonal convexa puede vigilarse con una única cámara
Tras esta primera experimentación podríamos preguntarnos si la conjetura se cumple para cualquier polígono no convexo. Entonces, pediríamos a los alumnos que construyan diferentes polígonos no convexos y que verifiquen si pueden vigilarse con una única cámara, y si esta puede estar situada en cualquier punto de la sala.
Por ejemplo, si disponemos de una sala como la representada por el applet 2 no será suficiente una sola cámara. El alumnado comprobaría esto experimentalmente al activar el rastro de PuntoPared: seleccionamos PuntoPared, pulsamos el botón derecho del ratón y marcamos la casilla Mostrar el rastro. Independientemente de dónde esté colocado el punto cámara, el alumnado comprueba que PuntoPared no alcanza a recorrer la totalidad de las paredes.
Applet 2
Al encontrar salas que necesitan más de una cámara, desechamos nuestra primera conjetura y nos surge la siguiente pregunta:
¿qué es lo que caracteriza a estas nuevas salas?
El alumnado suele responder a esta última cuestión diciendo que tienen picos. En lenguaje matemático, diremos que se trata de polígonos no convexos, es decir, hay al menos dos puntos del polígono que definen un segmento no contenido en el polígono. No estaría de más comentarles esta caracterización, para que se hagan una idea de cómo se formalizan ciertas ideas matemáticas. Como nuestro objetivo consiste en hallar el menor número de cámaras necesario, no nos queda más remedio que estudiar siempre el caso más problemático; es decir figuras no convexas con muchos picos. En este momento el profesor podría mostrar un polígono como el del applet 3 que tiene un único pico y que puede vigilarse con una sola cámara, si esta se sitúa en un lugar concreto. Como puede observarse en dicha figura, la cámara podría situarse en cualquier punto del trapecio , que resulta de la intersección del rectángulo y el triángulo , ya que desde esos puntos se puede trazar un segmento al resto de puntos de la sala sin que interfiera ninguna pared por medio.Applet 3
En polígonos con dos picos consecutivos que tienen un punto en común, como en el pentágono de la Figura 4 (el punto es común a los picos y ), los alumnos podrían también experimentar que toda la sala se puede vigilar con una única cámara situada en este caso en la intersección de los triángulos y .
En el caso de polígonos con dos picos consecutivos que no tienen ningún punto en común, sino que están unidos por un segmento, como por ejemplo, el hexágono de la Figura 4, se necesitarían como mínimo dos cámaras: una situada en cualquier punto del triángulo y otra en . Estas estructuras poligonales con picos consecutivos, unidos por segmentos, donde los triángulos que contienen a los picos no se intersecan entre sí, las denominaremos polígonos tipo rastrillo.
La experimentación con GeoGebra permite a los alumnos establecer la siguiente conjetura:
Las salas con estructura poligonal tipo rastrillo necesitan tantas cámaras como picos tienen para ser vigiladas
Figura 4a. Sala pentagonal
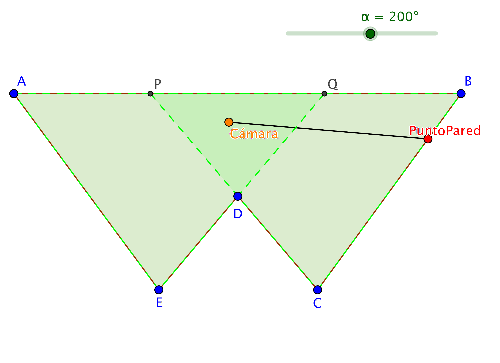
Figura 4b. Sala hexagonal.
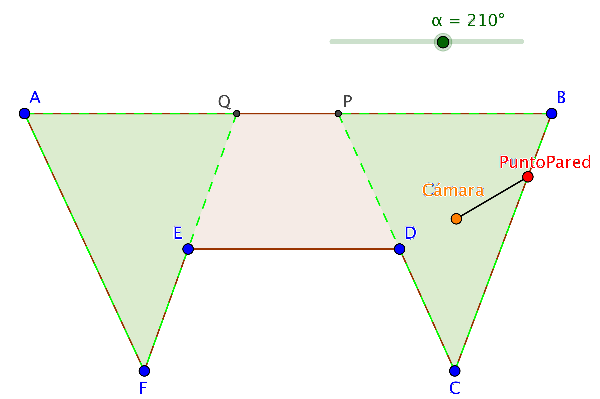
En el caso de polígonos con dos picos consecutivos que no tienen ningún punto en común, sino que están unidos por un segmento, como por ejemplo, el hexágono de la Figura 4, se necesitarían como mínimo dos cámaras: una situada en cualquier punto del triángulo AFQ y otra en PCB . Estas estructuras poligonales con picos consecutivos, unidos por segmentos, donde los triángulos que contienen a los picos no se intersecan entre sí, las denominaremos polígonos tipo rastrillo. La experimentación con GeoGebra permite a los alumnos establecer la siguiente conjetura:
Las salas con estructura poligonal tipo rastrillo necesitan tantas cámaras como picos tienen para ser vigiladas