Modifizierte Sinusfunktion
Mit diesem interaktiven Arbeitsblatt kannst du sehen, wie sich das Schaubild einer Sinusfunktion mit Hilfe verschiedener Parameter modifizieren lässt (Verschiebungen, Streckung, etc.)
Aufgabe:
a) Welche Parameter verschieben den Graphen, ohne dass seine Form verändert wird?
b) Welche Parameter verändern die Form des Graphen?
c) Skizziere die Funktion y(x)=3⋅sin(0,5⋅(x+π))
d) Skizziere die Funktion y(x)=−2⋅sin(2⋅(x+π/4)
e) Finde den Funktionsterm zu folgendem Graphen:
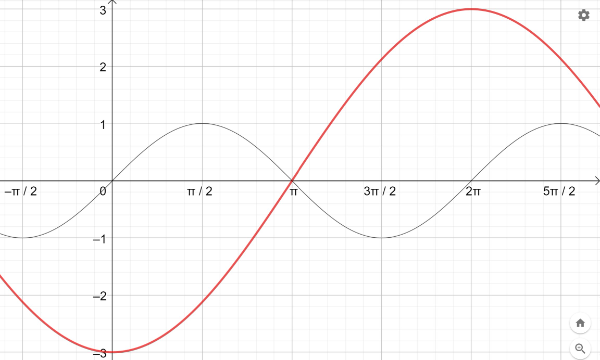
f) Finde den Funktionsterm zu folgendem Graphen:
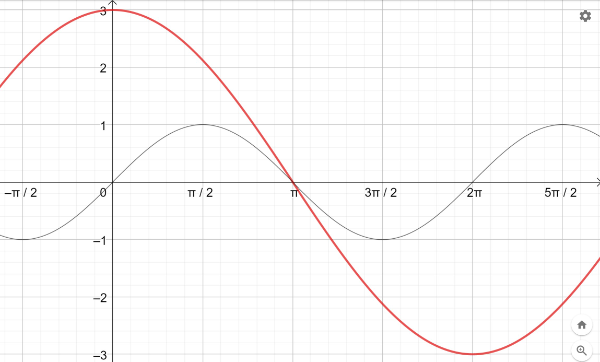
d)
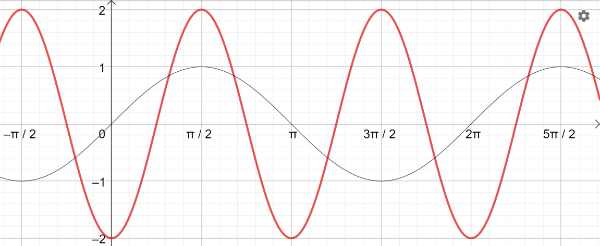
e) z.B. y(x)=3sin(0.5⋅x+3π/2) oder y(x)=3sin(0.5⋅x-π/2)
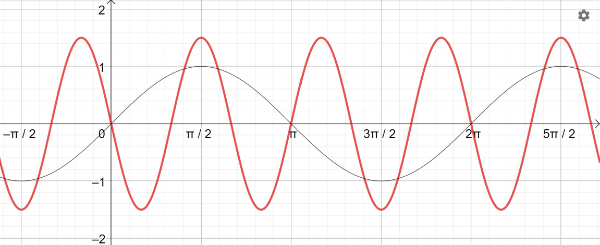
f) z.B. y(x)=-2sin(3x)