Polinomi, funzioni e proporzionalità (1ALSA)

Scrivi qui sotto un polinomio in cui ci sia solo la lettera x, di secondo grado, completo. Prova a farlo usando il comando fx "Inserisci formula" qui sotto a sinistra.

Apri GeoGebra Classico sul browser: https://www.geogebra.org/classic?lang=it Nella colonna di sinistra, dove c'è scritto "Inserimento" scrivi il polinomio che hai scelto. Per inserire gli esponenti usa l'apice ^ (shift+ì). Per scendere dall'esponente usa la freccetta verso destra della tastiera. Quando hai scritto clicca invio.

Cosa è stato disegnato? Prova a descrivere a parole tue cosa vedi.

Per intanto ti trovi in un piano cartesiano, credo tu già lo conosca. Il piano cartesiano è costruito da due rette, una orizzontale che si chiama asse delle x (o delle ascisse), e una verticale che si chiama asse delle y (o delle ordinate). Su di queste vedi i numeri: sull'asse x sono ordinati da sinistra a destra e sull'asse y dal basso verso l'alto. Le due rette si incontrano nel punto detto origine.

Ciascun punto del piano cartesiano è individuato dalle sue due coordinate (x,y), come se fosse il gioco della battaglia navale. Prima si legge il valore in corrispondenza dell'asse x orizzontale e poi il valore in corrispondenza dell'asse y verticale.

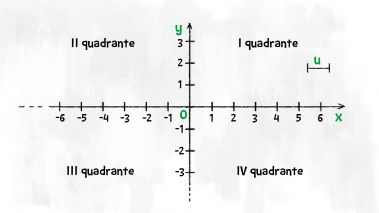
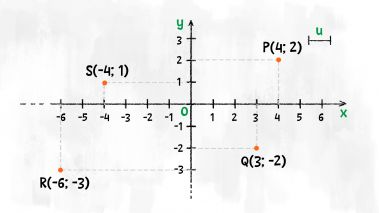
Torna alla scheda GeoGebra dove è disegnato il grafico del tuo polinomio. Scegli un punto della curva che sia esattamente all'incrocio di quadretti grossi e leggi le sue coordinate. Scrivile qui sotto.

Per controllare puoi scegliere il comando punto, nella barra orizzontale del menu di GeoGebra, quella sopra a dove hai scritto il polinomio: è la seconda casella (con il punto e la A), clicca e poi scegli "Punto" dal menu a tendina. Clicca con il mouse in corrispondenza del punto del grafico che stavi considerando: dovrebbero comparirti le coordinate che hai scritto qui sopra.

Adesso considera il valore della prima coordinata del punto, che corrisponde alla sua x. Nell'espressione del polinomio sostituisci questo valore alla x e calcola quanto fa. a) Che valore hai trovato? b) Quale y aveva il tuo punto?

Le tue risposte alle domande dovrebbero coincidere e questo perché i polinomio sono funzioni, cioè delle relazioni che associano elementi di un insieme a elementi di un altro insieme. A ogni x è associata una y: sostituendo il valore di x nel polinomio hai trovato la y del punto della funzione che aveva quella x. La regola perché si abbia una funzione è che TUTTI gli elementi dell'insieme da cui partono le frecce devono essere associati a UN SOLO elemento nell'insieme di arrivo delle frecce.

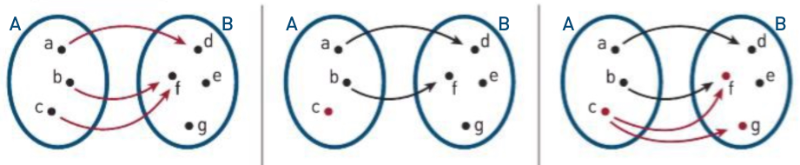
Per la regola qui sopra, spiega in ciascuno dei tre casi qui sopra rappresentati se l'insieme delle frecce che parte dall'insieme di sinistra e raggiunge quello di destra corrisponde a una funzione oppure no.

Anche i polinomi sono funzioni: per ciascun valore di x che inserisco nel polinomio trovo un solo valore, che hai visto essere il valore della y del punto sul grafico! GeoGebra fa anche da calcolatrice. Guarda un altro punto sul grafico e pensa alle sue coordinate. Scrivi nella colonna di sinistra f() mettendo tra parentesi il valore della coordinata x del punto. Dovrebbe comparire il valore della seconda coordinata del punto. Prova a farlo per altri valori di x e vedrai che sarà sempre giusto.

Sentirai molto parlare di funzioni d'ora in poi, anche in altre materie. Per esempio in Fisica userete molto i concetti di grandezze direttamente e inversamente proporzionali, cioè legate da particolari funzioni.

Facciamo un esempio di grandezze direttamente proporzionali. C'è un rettangolo che ha altezza 2 e questa è fissa. La base invece cambia. a) Quando la base è 1, quanto è l'area del rettangolo? b) Quando la base è 2? c) Quando la base è 3? d) Quando la base è 4? e) Elenca le coppie di valori (base, area) che hai trovato. f) Cosa puoi dire che hanno in comune tutte queste coppie?

Torna pure su GeoGebra e clicca i pallini colorati nella colonna a sinistra dello schermo così che scompaia cosa hai fatto finora. Ora con il comando Punto usato prima, clicca sui punti che hai elencato al punto e) della scorsa domanda, cioè i punti che hanno come coordinate rispettivamente il valore della base e il valore dell'area corrispondente.

a) In che modo si dispongono i punti nel piano cartesiano? b) Clicca sulla terza casellina del menu di GeoGebra e usa il comando "Retta": clicca su due dei punti. Cosa succede? c) Che equazione è comparsa a sinistra nella barra degli inserimenti? In che modo è legata alla risposta che hai dato al punto f) della scorsa domanda?

Due grandezze sono direttamente proporzionali quando il loro rapporto è costante. La relazione fra due grandezze y e x direttamente proporzionali, tali che la y dipende dalla x, si scrive nella forma

y = kx

in cui k è detta costante di proporzionalità. Notiamo che se x raddoppia allora y raddoppia, se x triplica allora y triplica e così via. Il grafico cartesiano di una relazione di proporzionalità diretta è una retta passante per l’origine degli assi.

a) Quanto vale k nel nostro esempio? b) Cosa avevi risposto al punto c) della domanda precedente?

Facciamo adesso un esempio di grandezze inversamente proporzionali. C'è un rettangolo che ha area 24 e questa è fissa. La base e l'altezza invece cambiano. a) Quando la base è 1, quanto è l'altezza del rettangolo? b) Quando la base è 2? c) Quando la base è 3? d) Quando la base è 4? e) Quando la base è 6? f) Elenca le coppie di valori (base, altezza) che hai trovato. g) Cosa puoi dire che hanno in comune tutte queste coppie?

Fai su GeoGebra lo stesso lavoro fatto con le grandezze direttamente proporzionali: disegna i punti che hanno come coordinate rispettivamente il valore della base e quello dell'altezza. a) Prova a descrivere come si dispongono. Usa la settima casellina del menu e il comando "Conica - 5 punti": clicca sui cinque punti. b) Che equazione è comparsa a sinistra nella barra degli inserimenti? In che modo è legata alla risposta che hai dato al punto g) della scorsa domanda?

Due grandezze sono inversamente proporzionali quando il loro prodotto è costante. Si scrive

xy = k

in cui k è detta costante di proporzionalità inversa. Notiamo che se x raddoppia allora y si dimezza, se x triplica allora y diventa un terzo e così via. Il grafico cartesiano di una relazione di proporzionalità inversa è un arco di iperbole equilatera.

a) Quanto vale k nel nostro esempio? b) Cosa avevi risposto al punto b) nella risposta precedente?

Se hai già finito, puoi intrattenerti con il gioco della Torre di Hanoi che avevamo visto in classe qualche tempo fa.

Polinomi, funzioni e proporzionalità (1ALSA)

Nuove risorse

Scopri le risorse

Scopri gli argomenti