Quadrats dins quadrats
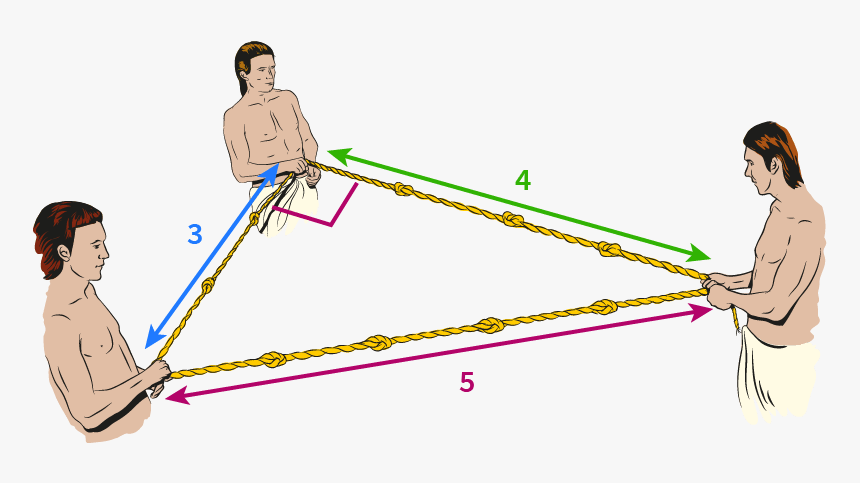
Segons Heròdot, a l’Antic Egipte hi havia els mesuradors de cordes, que dotats únicament de cordes amb molts nusos sempre a una mateixa distància eren capaços de mesurar amb gran habilitat les àrees dels terrenys agrícoles, després d’una crescuda del Nil. Se’ls considera a vegades els primers geòmetres de la història (literalment, Geo-metria: mesura de la terra).
Una de les estratègies que utilitzaven era la següent: si prenem una longitud de 12 nusos i els disposem en forma de triangle, amb 3 nusos, 4 nusos, i 5 nusos, aleshores l’angle format entre els 3 i els 4 nusos ha de ser recte (de 90o)
Feu la comprovació amb Geogebra per veure si aquest angle és recte.
Per què això és cert?
Fixa't en aquesta imatge.
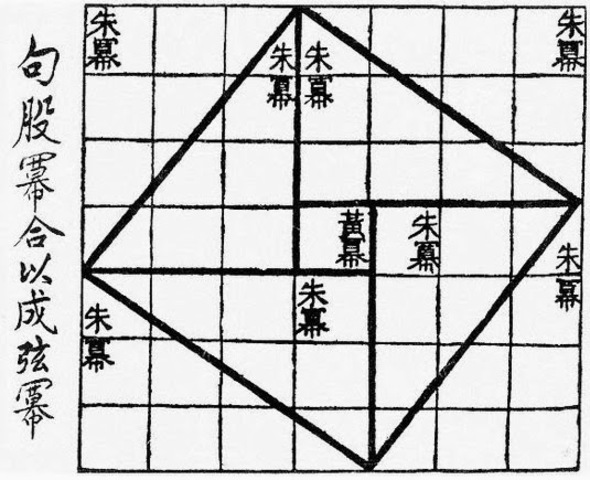
A partir del triangle anterior i el diagrama xinès que teniu, modelitzeu amb el Geogebra aquesta construcció.
Senyala totes les afirmacions correctes
Quant mesura l'àrea del quadrat intern?