Quadratische Gleichungen
Du hast bereits die allgemeine Form einer quadratischen Funktion kennengelernt. Wie sah die doch gleich aus?
Du kennst auch schon einen weiteren Funktionstypen: Die linearen Funktionen, machen wir eine kurze Wiederholung dazu. Wie sah hier nochmal der Funktionsterm aus?
Lies im folgenden Diagramm Steigung und y-Achsenabschnitt der Gerade ab und ergänze dann den Funktionsterm unter dem Diagramm.
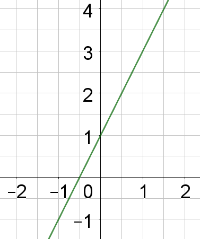
Genau wie bei Parabeln konnten wir auch linearen Funktionen eine Nullstelle zuordnen. Ermittle graphisch die x-Koordinate der Nullstelle.
Auch rechnerisch kann man die Nullstelle berechnen. Gib die entsprechende Gleichung an:
Gehen wir nun zurück zu den quadratischen Funktionen. Wir wollen auch hier die Nullstellen bestimmen. Lies die Nullstellen der Funktion mit vom Graphen ab.
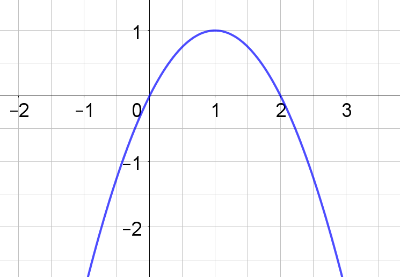
Stelle auch hier wieder eine Gleichung auf, mit der sich diese Nullstellen berechnen lassen.
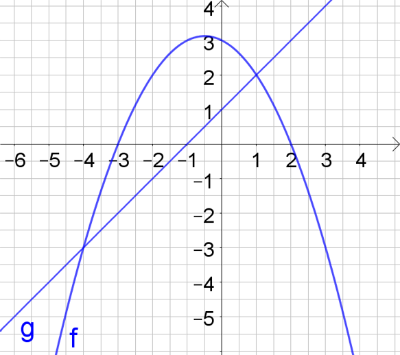
Du siehst die Graphen der Funktionen und . Gib eine Gleichung an, deren Lösungen den Schnittstellen der Graphen entspricht.