Ecuación Exponencial
Recordad que en las ecuaciones exponenciales la incógnita se encuentra en el exponente de potencias.
En este texto vamos a ver tres métodos distintos para resolver ecuaciones exponenciales:
- Aplicación de las propiedades de las potencias (método básico)
- Aplicación de logaritmos
- Aplicación de un cambio de variable
Método 1
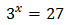 Cuando la ecuación es una igualdad entre una exponencial y un número, debemos intentar escribir el número y la base de la exponencial como una potencia con base común.
En nuestra ecuación, podemos escribir 27 como una potencia de 3:
Cuando la ecuación es una igualdad entre una exponencial y un número, debemos intentar escribir el número y la base de la exponencial como una potencia con base común.
En nuestra ecuación, podemos escribir 27 como una potencia de 3:
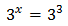
Tenemos una igualdad entre dos potencias con la misma base. Para que la igualdad sea cierta, ambas potencias deben tener el mismo exponente:
Tenemos una igualdad entre dos potencias con la misma base. Para que la igualdad sea cierta, ambas potencias deben tener el mismo exponente:
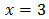
Por tanto, la solución de la ecuación es x = 3.
Más ecuaciones exponenciales básicas resueltas
Por tanto, la solución de la ecuación es x = 3.
Más ecuaciones exponenciales básicas resueltasMétodo 2
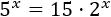
Si no podemos escribir en la ecuación potencias con bases comunes, no podremos igualar los exponentes para hallar la incógnita. Es en estos casos cuando aplicamos logaritmos y sus propiedades.
En nuestra ecuación tenemos las bases 2 y 5, que son distintas, así que aplicaremos logaritmos.
Pueden utilizarse logaritmos en cualquier base, nosotros lo haremos en base 10 ya que es la que suele emplearse habitualmente.
Aplicamos logaritmos en base 10 en ambos lados de la ecuación:
Si no podemos escribir en la ecuación potencias con bases comunes, no podremos igualar los exponentes para hallar la incógnita. Es en estos casos cuando aplicamos logaritmos y sus propiedades.
En nuestra ecuación tenemos las bases 2 y 5, que son distintas, así que aplicaremos logaritmos.
Pueden utilizarse logaritmos en cualquier base, nosotros lo haremos en base 10 ya que es la que suele emplearse habitualmente.
Aplicamos logaritmos en base 10 en ambos lados de la ecuación:
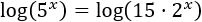
Aplicando la propiedad "el logaritmo del producto es la suma de los logaritmos", el logaritmo del lado derecho podemos escribirlo como una suma:
Aplicando la propiedad "el logaritmo del producto es la suma de los logaritmos", el logaritmo del lado derecho podemos escribirlo como una suma:
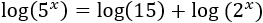
Extraemos los exponentes de los logaritmos (propiedad de los logaritmos):
Extraemos los exponentes de los logaritmos (propiedad de los logaritmos):
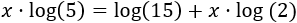
Escribimos en el lado izquierdo los sumandos que tienen la incógnita:
Escribimos en el lado izquierdo los sumandos que tienen la incógnita:
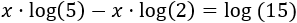
Finalmente, extraemos factor común y despejamos la incógnita:
Finalmente, extraemos factor común y despejamos la incógnita:
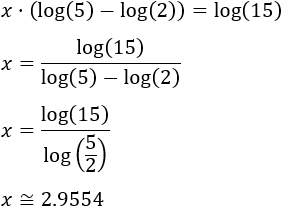 Más ecuaciones exponenciales resueltas con logaritmos
Más ecuaciones exponenciales resueltas con logaritmosMétodo 3
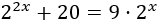 El método de cambio de variable se aplica cuando la incógnita tiene coeficiente distinto de 1. Por ejemplo, en el lado izquierdo de la ecuación tenemos el exponente 2x, cuyo coeficiente es 2.
Como la exponencial que tenemos en la ecuación es , aplicamos el cambio de variable . Esto significa que vamos a escribir una donde aparece :
El método de cambio de variable se aplica cuando la incógnita tiene coeficiente distinto de 1. Por ejemplo, en el lado izquierdo de la ecuación tenemos el exponente 2x, cuyo coeficiente es 2.
Como la exponencial que tenemos en la ecuación es , aplicamos el cambio de variable . Esto significa que vamos a escribir una donde aparece :
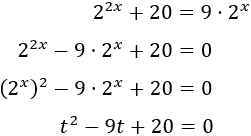
Tenemos una ecuación de segundo grado cuyas soluciones son
Tenemos una ecuación de segundo grado cuyas soluciones son
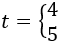
Como , entonces tenemos
Como , entonces tenemos
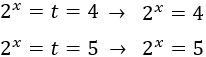 De la primera ecuación tenemos la solución x=2. De la segunda ecuación obtenemos una solución logarítmica:
De la primera ecuación tenemos la solución x=2. De la segunda ecuación obtenemos una solución logarítmica:
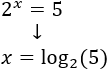
Más información
- Introducción a las exponenciales
- Ecuaciones exponenciales (sin logaritmos)
- Ecuaciones exponenciales (con logaritmos)
- Propiedades y ejercicios de potencias
- Fracciones equivalentes y fracción irreductible
- Resolución de ecuaciones
- Problemas con sistemas de ecuaciones
- Teorema de Pitágoras (Problemas)
- Calculadora de Pitágoras
- Progresiones aritméticas y geométricas
- Ecuaciones de segundo grado
- Calculadora de porcentajes
- ProblemasYecuaciones.com
- Ecuaciones Resueltas