8. Distancia de un punto a una recta / distancia entre rectas

Integrantes

Bustos Rangel Luis Roberto Noriega Zaldivar Jorge Armando Ortiz Marin Jazmine Saavedra Linares Abigail Sánchez Esparza Mariana

8.1: De un PUNTO a una RECTA

Consideremos en el espacio a una recta "L" (L : (x,y,z) = P + tu) y un punto "Q". Queremos hallar una expresión para la distancia d mínima entre L y Q, también el punto Q' el cuál será el punto en la recta en la que se alcanza esta distancia mínima. Q' será la proyección ortogonal de Q a la recta L. Una forma de conseguir esto es usando el área del paralelogramo.

Para calcular esto, consideremos un punto P sobre la recta L y un vector director u. El área del paralelogramo determinada por el vector PQ y por u es el módulo vectorial de ambos vectores.

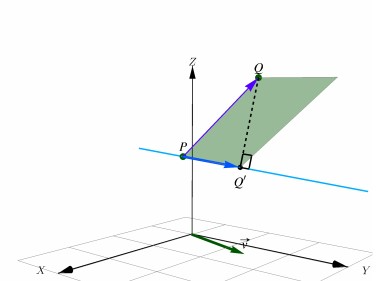
||PQ x u||

El área de un paralelogramo también viene dada por el producto de la Base por la Altura, entonces:

||u||d(Q,L)

Por lo tanto: d(Q,L)=

Otro método que podemos usar para encontrar la distancia es usando el cálculo algebraico. Como d(Q,L) = d(Q,Q') con Q'=P+t_mu y como QQ'u entonces:

(Q-Q')u=0 (Q-P-t_mu)u=

De aquí obtenemos que d(Q,L)=d(Q,Q') con Q'=P+ = P+proy_u^PQ

Con este método podremos encontrar el punto de proyección de el punto Q sobre la recta L, es decir Q'.

Aprende más sobre esta fórmula:

8.1 Distancia de un punto a una recta 2.0

Veamos el siguiente planteamiento tenemos en R3, en el espacio, una recta y un punto exterior (P1). La recta la tenemos definida por un punto P0 y su vector director L: { P0, d->}.

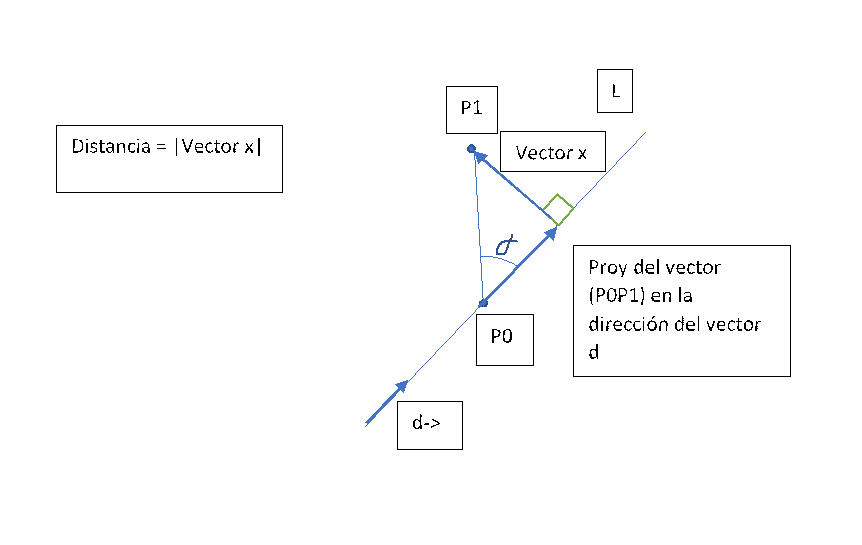
Necesitamos saber la distancia más corta entre la recta y él punto P1, para eso podemos usar un triángulo rectángulo (cateto adyacente, cateto opuesto, hipotenusa, ángulo Alpha) y podemos proyectar el vector director al punto P0 y el P1 al P0 con el producto escalar P1P0 y el coseno del ángulo. Puedo plantear que si sé cuanto es: el vector x el vector Proyección (P0P1) = P0P1; podemos despejar el vector x y calcular su módulo Vector P0P1 = vector Proy (vector P0P1) dirección vector d +vector x Vector P0P1 – Proy (P0P1) dirección vector d = Vector X Proy (P0P1) dirección vector d = |Vector P0P1| * cos ángulo Alpha; Y esto sale del producto escalar

8.2: Distancia entre DOS RECTAS

Se refiere a la distancia mínima que existe entre cualquier punto de una recta con cualquier punto de la otra recta. Esta distancia corresponde a la longitud del segmento ortogonal a ambas rectas que va de una recta a otra.

Dadas 2 rectas diferentes L₁: (x,y,z) = P + tv y L₂: (x,y,z) = Q + tu siempre será posible encontrar 2 planos paralelos (siempre y cuando las rectas no se crucen en ningún punto, en cuyo caso la distancia entre ellas sería igual a 0)

₁y

₂que contienen a L₁y L₂, respectivamente. El vector normal a estos 2 planos es u

Sabemos que d(L₁,L₂)=d(P,

₂), P

L₁

₁, En detalle sería: Un vector normal para

₂ es n=u

v y Q

₂entonces:

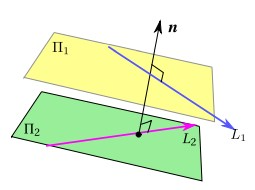
d(L₁,L₂)=d(P,₂)=

Otro método que te podría interesar:

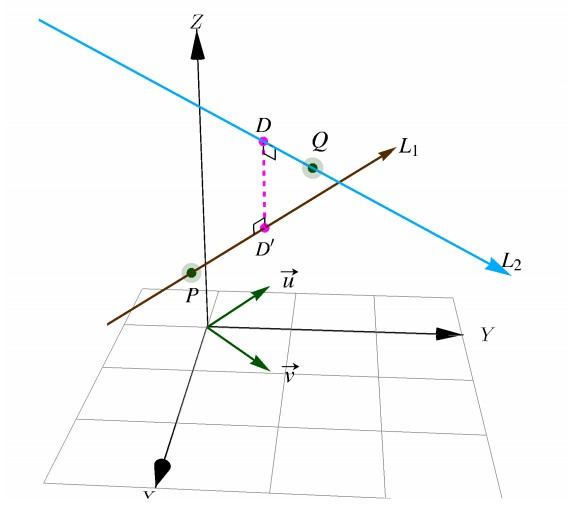
8.2 Distancia entre 2 rectas paralelas

Veamos el siguiente planteamiento tenemos en R3, en el espacio, una recta L1 y una recta L2. La recta L1 la tenemos definida por un punto P1 y su vector director d1: {P1, d1->} L2 {P2, d2->}

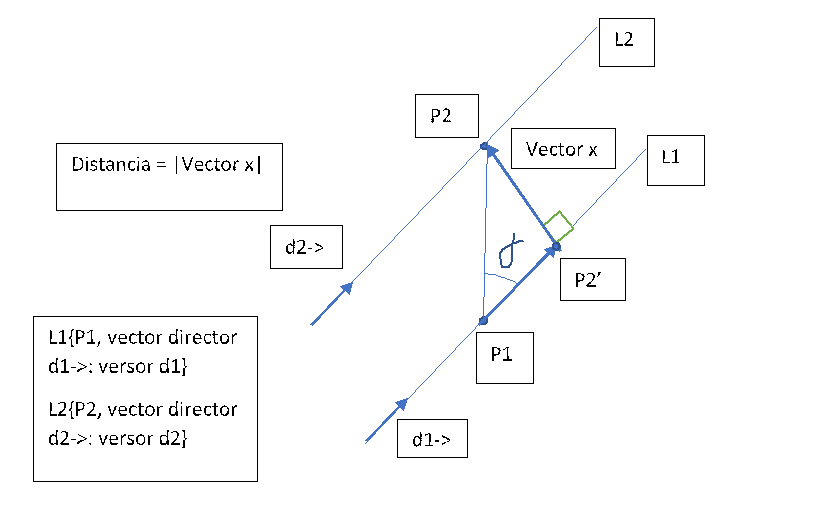
Necesitamos saber la distancia más corta entre la recta L1 y la recta L2, para eso podemos usar un triángulo rectángulo (cateto adyacente, cateto opuesto, hipotenusa, ángulo Alpha) y podemos calcular el vector x, restando: vector P1P2 – vector P1P2’ = vector x Vector P1P2’ = vector Proyeccion vectorial (vector P1P2) sobre el vector versor d1 Vector P1P2 – (vector P1P2 Producto escalar versor d1) * Versor d1 = Vector X (vector P1P2 Producto escalar versor d1) = Escalar (vector P1P2 Producto escalar versor d1) * Versor d1 = proyección vectorial Distancia = |vector x|

Sobre la distancia entre un punto y una recta...

Calcula la distancia entre el punto P=(2,4,1) y la recta r:(x,y,z)=(2,3,-1)+t(1.2.1)

Select all that apply

A
B
2.333333
C

Check my answer (3)

Sobre la distancia entre dos rectas...

Calcula la distancia entre las rectas r: y r':