Teorema
La bisettrice di un angolo è il luogo dei punti dell'angolo che sono equidistanti dai lati dell'angolo.
In base alla definizione di luogo geometrico, per dimostrare questo teorema, si devono dimostrare due proposizioni diverse:
- tutti i punti appartenenti alla bisettrice di un angolo sono equidistanti dai lati dell'angolo;
- tutti i punti del piano equidistanti dai lati dell'angolo appartengono alla bisettrice.
Dimostrazione 1
Ipotesi:
P appartiene alla bisettrice di
Tesi:
Dim:
| I due triangoli rettangoli POH e POK sono congruenti per il 2° criterio generalizzato di congruenza, dato che: OP è in comune, gli angoli POH e POK sono concongruenti perchè OP è la bisettrice di . Pertanto, perchè elementi corrispondenti in triangoli congruenti. |
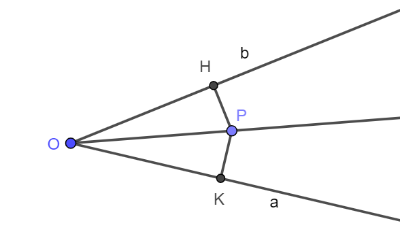
Dimostrazione 2
Ipotesi:
Tesi: P appartiene alla bisettrice di
Dim:
I triangoli rettangoli POH e POK hanno ordinatamente congruenti l'ipotenusa e un cateto:
OP è in comune;
per ipotesi.
Pertanto, sono congruenti per il criterio di congruenza dei triangoli rettangoli.
In particolare, perchè sono elementi corrispondenti in triangoli congruenti.
Quindi, P appartiene alla bisettrice dell'angolo .