circles? circle-geometry?
Diese Aktivität ist eine Seite des geogebrabooks Möbius-Werkzeuge circle tools (November 2018)
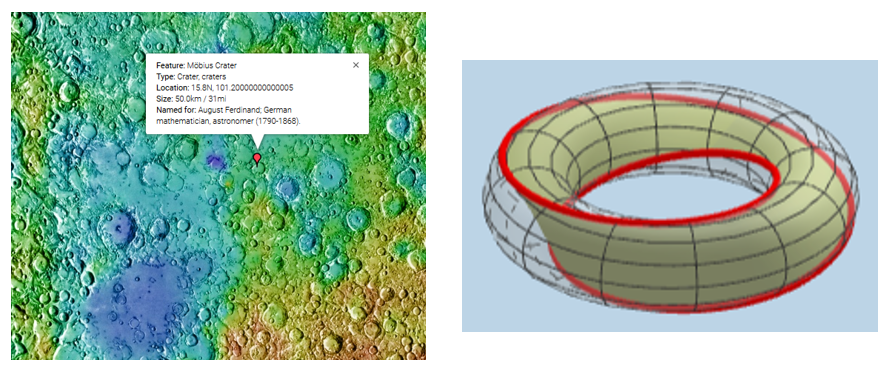
Nach August Ferdinand Möbius (*1790; 1868 in Leipzig) ist nicht nur ein Mond-Krater oder das Möbiusband benannt, sondern auch die Möbius-Geometrie: d.i. die Geometrie der Kreise. Kreise in der Ebene können sich schneiden oder berühren oder nicht schneiden. Wenn sie sich schneiden, kann man den Winkel zwischen ihnen messen. In besonderen Fällen können zwei Kreise sich orthogonal schneiden. Nimmt man die Geraden als Kreise durch einen gedachten Punkt hinzu, ist man in der Möbius-Geometrie angelangt. Die Beziehungen zwischen Kreisen kann man sich ohne die lästige Unterscheidung zwischen Geraden und Kreisen auf der RIEMANNschen Zahlenkugel verdeutlichen: Kreise sind die Schnitte der Ebenen mit der Kugel. Zwischen den beiden Darstellungen vermittelt die stereographische Projektion. Man verläßt die EUKLIDische Welt mit Hilfe der Kreis-Spiegelungen
, oft als Inversion am Kreis
bezeichnet: dabei werden aus Geraden Kreise, die Abstände spielen keine solche Rolle mehr,
aus Großem wird winzig Kleines.
Nicht-EUKLIDische Fragen stellen sich:
- Orthogonale Kreise von einem Punkt aus zu einem vorgegebenen Kreis konstruieren
- Berühr-Kreise von einem Punkt aus an einen vorgegebenen Kreis legen
- Symmetrien zu zwei Kreisen konstruieren
- Berührkreise an zwei vorgegebene Kreise legen
- wann und wie liegen 4 Punkte auf einem Kreis?
- Konstruiere alle Kreise, die drei vorgegebene Kreise berühren
gebra-books ist für eine spezielle Lage der drei Kreise die Lösung angezeigt!
Ge
gebra stellt einige Werkzeuge für Kreiskonstruktionen zur Verfügung.
Wir wollen für MÖBIUS-Geometrie-Interessierte in diesem book
weitere Werkzeuge (test circle tools) vorstellen.
Für Experten: Die Gruppe der gleichsinnigen MÖBIUS-Transformationen ist isomorph zur Gruppe der
gebrochen-linearen Abbildungen der komplexen GAUSSschen Zahlenebene: diese Abbildungen sind kreis- und winkeltreu.
Für die komplexe Funktionentheorie ist die MÖBIUS-Geometrie nicht ganz uninteressant.
Lineare Kreisbüschel und die dazu orthogonalen Kreise können gut mit komplex-analytischen Funktionen realisiert werden.Die Funktion bildet die Achsenparallelen und
auf die Kreise durch bzw. um und ab.