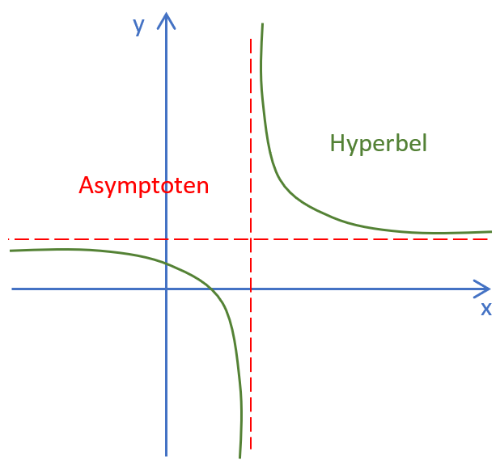
Eigenschaften elementarer gebrochen-rationaler Funktionen
Lernziele:
Graphen gebrochen-rationaler Funktionen erkennen und mit Fachbegriffen beschreiben
mithilfe von Wertetabellen Graphen gebrochen-rationaler Funktionen zeichnen
Asymptoten bestimmen
die Definitionsmenge gebrochen-rationaler Funktionen angeben
Was ist eine gebrochen-rationale Funktion?
Du kennst schon die rationalen Zahlen . Diese enthalten alle Zahlen, die als Bruch geschrieben werden
können, also alle positiven und negativen ganzen Zahlen und alle positiven und negativen Brüche.
Das „gebrochen-rational" bezieht sich also auf einen Bruch im Funktionsterm. Doch dieser Bruch muss eine besondere Eigenschaft haben, damit man die Funktion „gebrochen-rational“ nennt.
Einstiegsaufgabe:
Nimm die Funktionsgleichungen unten in beliebiger Reihenfolge „unter die Lupe“ (d.h. ziehe sie auf die Lupe) und finde heraus, ob sie gebrochen-rational sind oder nicht, indem du noch einmal auf die Funktionsgleichung in der Lupe klickst.
Findest du heraus, was die gebrochen-rationalen Funktionsterme im Gegensatz zu den anderen Funktionstypen gemeinsam haben?
Funktionen unter der Lupe
Vermutung:
Nun fertigen wir einen Hefteintrag an. Schreibe alles ab, was blau ist.
Fülle die Lücken mit deinen Erkenntnissen und Beispielen aus der Einstiegsaufgabe.
III. Elementare gebrochen-rationale Funktionen
III.1 Eigenschaften gebrochen-rationaler Funktionen
Definition: Hat der Term einer Funktion eine Variable ________________________________, so nennt man die Funktion gebrochen-rational. Einen solchen Term nennt man Bruchterm.
z.B.: _____________________________________________________________________ (Hinweis: Übernimm hier einfach 2-3 gebrochen-rationale Funktionen aus der Einstiegsaufgabe als Beispiele)
Zahlen, für die der Nenner Null wird, gehören nicht zur Definitionsmenge, weil der Funktionsterm an dieser Stelle nicht definiert ist und ihnen kein Wert zugeordnet werden kann. Man nennt sie Definitionslücken.
Lösung: Klicke einfach auf "Antworten überprüfen"
Aufgabe: S. 61/4
Bestimme die Definitionslücken der folgenden Funktionsgleichungen in deinem Übungsheft und gib die maximale Definitionsmenge an. Überprüfe deine Ergebnisse anschließend hier, indem du sie in die Felder eingibst.
z.B. \ {-3}
a) Definitionslücke bei x =
b) Definitionslücke bei x =
c) Definitionslücke bei x =
d) => Definitionslücke bei x =
e) Defnitionslücke bei x =
f) Definitionslücke bei x =
g) Defnitionslücke bei x =
h) Definitionslücke bei x =
i) Defnitionslücke bei x =
Graphen gebrochen-rationaler Funktionen
Du hast schon Graphen gebrochen-rationaler Funktionen gesehen. Klaus dagegen anscheinend nicht. Er
hat die Funktionsvorschrift gegeben und dazu eine Wertetabelle erstellt:
Mithilfe derer zeichnet er folgenden Graphen:
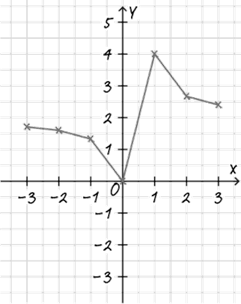
Aufgabe: a) Sieh dir den Funktionsterm noch einmal an und bestimme die Definitionslücke. Dieser Lücke wird kein Funktionswert zugeordnet! Definitionslücke: x =
Taucht sie in Klaus‘ Wertetabelle auf?
a) Plotte nun selbst die Funktion und beschreibe kurz in deinem Übungsheft den Verlauf der Funktion links und rechts von der Definitionslücke. Nutze dazu die Zoom-Funktion des Plotters.
Benenne den Fehler, den Klaus gemacht hat.
Hinweis: Klicke "Antworten überprüfen", um einen Hinweis zu erhalten.
Und weiter geht es mit dem Hefteintrag:
Graph:
Bei Definitionslücken haben die Graphen gebrochen-rationaler Funktionen so genannte senkrechte Asymptoten. Das sind Geraden, denen sich der Graph beliebig anschmiegt, ohne sie zu berühren.
Aufgabe: Betrachte noch einmal den eben geplotteten Graphen. Siehst du auch noch eine waagrechte Asymptote? Hinweis: Klicke "Antworten überprüfen", um einen Hinweis zu erhalten.
Gleichung der waagrechten Asymptote: y =
Aufgabe:
a) Setze nun sehr große Werte (1000, 10.000, 100.000) und sehr kleine Werte (-1000, -10.000,
100.000) in die Funktionsgleichung von oben, , ein, und berechne die Funktionswerte.
Notiere dir die Ergebnisse auch in deinem Übungsheft und beschreibe dort (gerne auch stichpunktartig, aber nachvollziehbar) deine Beobachtungen.
b) Stelle eine Hypothese auf, woran du am Funktionsterm die waagrechte Asymptote erkennen kannst, und schreibe diese ebenfalls in dein Heft.
Überprüfe deine Hypothese, indem du in die folgenden drei Funktionsgleichungen ebenfalls die Werte +/-1000, +/- 10.000 und +/- 100.000 einsetzt und einen Bezug zu den Termen herstellst:
, und
Gleichungen der waagrechten Asymptoten der Funktionen a, b und c:
Der letzte Teil des Hefteintrags in diesem Abschnitt:
Merke: Den Graphen einer gebrochen-rationalen Funktion nennt man Hyperbel. Er besteht aus zwei nicht
verbundenen Ästen, die punktsymmetrisch zum Schnittpunkt der Asymptoten des Graphen sind.
Skizze: (bitte auch ins Schulheft übernehmen!)
