Lekcija 2.
Da bismo došli do formule za površinu valjka, prvo je potrebno da otkrijemo kako izgleda mreža valjka.
Mreža valja sadrži dva kruga koja su podudarna njegovim osnovama, dok je omotač valjka razvijen u ravni
ustvari pravougaonik.
Dužina jedne stranice pravougaonika koji predstavlja omotač jednaka je visini valjka,
dok je dužina druge stranice pravougaonika jednaka obimu osnove.
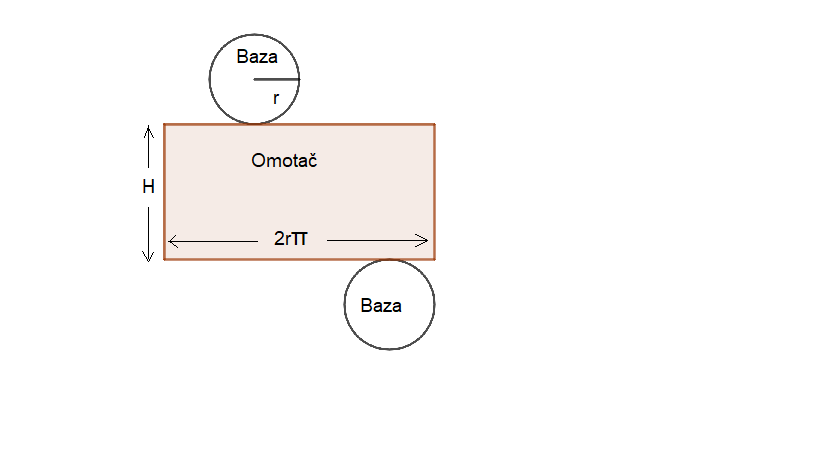
Neka je:
- poluprečnik valjka
- visina valjka
- površina osnove valjka
- površina omotača valjka
Tada je:
i
pa je onda površina valjka:
Dakle, površina valjka poluprečnika osnove r i visine H izračunava se po formuli:
Primer 1.
Izračunajmo površinu valjka čija je visina , a poluprečnik osnove .
Koristeći date podatke i uvrštavajući ih u formulu za površinu valjka dobijamo sledeće:
Ako se uzme da je , dobija se približna vrednost površine .
Zadatak 1.
Odredi visinu valjka ako je poluprečnik osnove , a njegova površina
Zadatak 2.
Stranice pravougaonika su i .
Odredi površinu tela koje nastaje rotacijom:
a) oko stranice ;
b) oko stranice .
Domaći zadatak:
1. Površina valjka je , a površina njegovog omotača je . Izračunati dužinu visine valjka.
2. Površina omotača valjka je , a visina valjka je dva puta veća od poluprečnika. Odrediti poluprečnik i visinu tog valjka.
3. Osni presek valjka je kvadrat površine . Izračunati površinu tog valjka.