Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

L1.20 - Transformations, Transversals, and Proof

Author:Ms. Leon-Guerrero (Ms. LG)

Learning Intentions and Success Criteria

We are learning to:
  • Prove (in writing) that when a transversal crosses parallel lines, alternate interior angles are congruent.
  • Prove that when a transversal crosses parallel lines, corresponding angles are congruent.
We are successful when we can:
  • Prove alternate interior angles are congruent.
  • Prove corresponding angles are congruent.

20.1: Math Talk: Angle Relationships

20.1: Math Talk: Angle Relationships

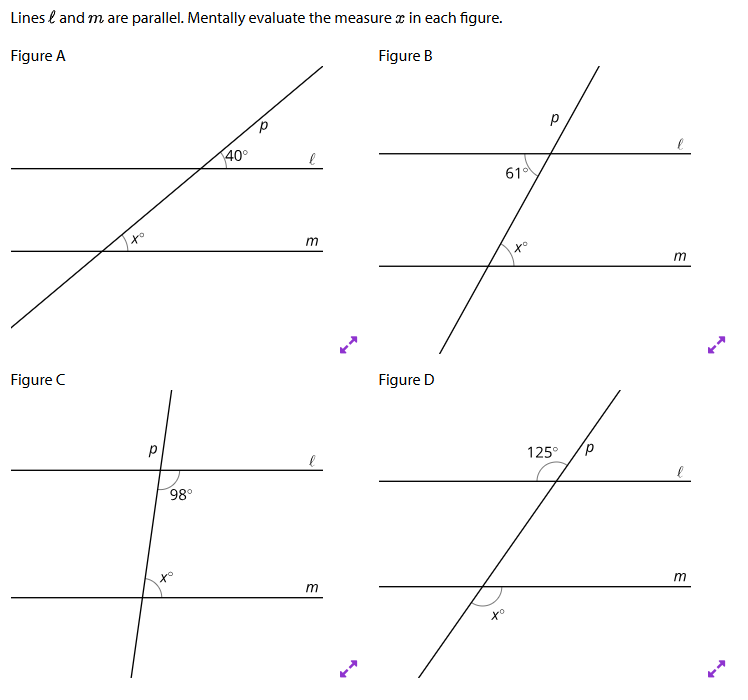
20.2: Make a Mark? Give a Reason.

1. Translate lines AE and CD by the directed line segment from B to C. Label the images of A, B, C, D, E as A’, B’, C’, D’, E’. 2. What is true about lines AE and A’E’? Explain your reasoning.

3. Take turns with your partner to identify congruent angles.

  • For each pair of congruent angles that you find, explain to your partner how you know the angles are congruent.
  • For each match that your partner finds, listen carefully to their explanation. If you disagree, discuss your thinking and work to reach an agreement.

20.3: An Alternate Explanation

1. Rotate line AE by 180 degrees around point C. Label the images of A, B, C, D, E as A’, B’, C’, D’, E’. 2. What is true about lines AB and A’B’? Explain your reasoning.

3. Take turns with your partner to identify congruent angles.

  • For each pair of congruent angles that you find, explain to your partner how you know the angles are congruent.
  • For each match that your partner finds, listen carefully to their explanation. If you disagree, discuss your thinking and work to reach an agreement.

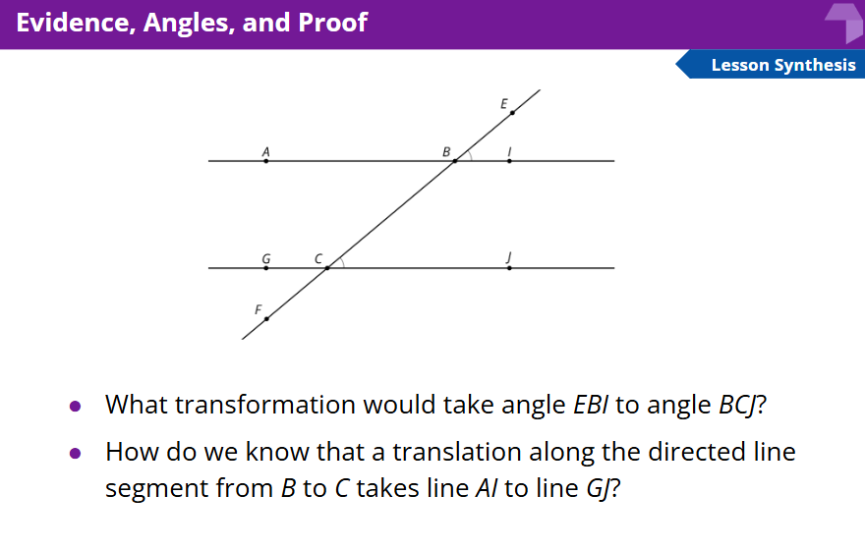
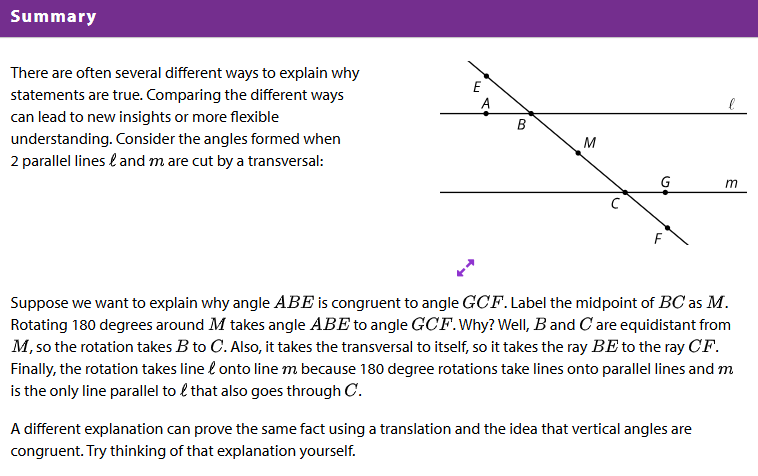
Image
Image
Image

Learning Intentions and Success Criteria

We are learning to:
  • Prove (in writing) that when a transversal crosses parallel lines, alternate interior angles are congruent.
  • Prove that when a transversal crosses parallel lines, corresponding angles are congruent.
We are successful when we can:
  • Prove alternate interior angles are congruent.
  • Prove corresponding angles are congruent.
Image

Cool-Down: Transformations on Parallel Lines

1.

2.

New Resources

Discover Resources

Discover Topics