Maximum/minimum d'une fonction
Énoncé possible pour les élèves
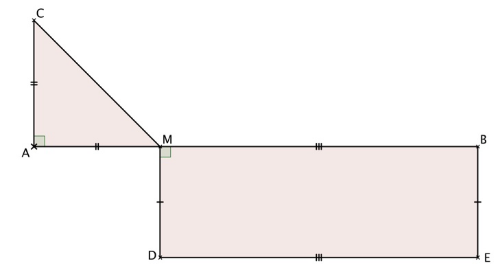
M est un point du segment [AB].
De part et d’autre du segment [AB] sont représentés :
• un triangle AMC rectangle et isocèle en A ;
• un rectangle MDEB.
On a : AB = 16 ; BE = 4
1 – Construire une figure dynamique sur Geogebra permettant de modéliser cette situation.
2 – Où faut-il placer M pour que l’aire totale du massif soit minimale ? Combien mesure cette aire ?
Aide :
• Pour calculer l’aire totale, écrire dans la ligne de saisie : Aire_totale=triangle1+quadri1 (triangle1 et quadri1 sont les noms des 2 polygones)
• On pourra ensuite créer un point de coordonnées (AM;Aire_totale) dans un repère pour visualiser l’aire maximale
Indication pour tracer la figure :
1 – Tracer en premier ce qui est fixe : ici le segment [AB] de longueur 16 et la segment [BE] de longueur 4 et perpendiculaire à (AB)
2 – Placer ce qui est mobile : ici le point M mais il sera « lié » au segment [AB]
3 – Construire les points C et D. Reporter la distance AM se fait « simplement » en utilisant l’outil Cercle (Centre, Point).
3 – Construire le reste de la figure en conservant les propriétés de celle-ci.
4 – L’affichage du point M (question 2) peut se faire sur la même vue (Vue Graphique) ou sur une deuxième vue (Graphique 2) qui peut être affiché grâce au menu Affichage→Graphique2.