Das Volumen des Spats
Hopp Hopp Hopp Mario!
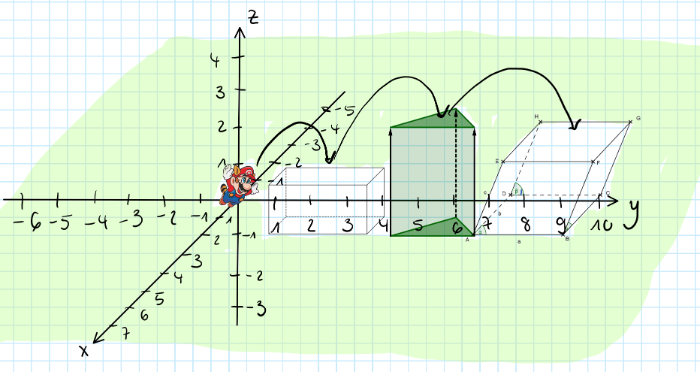
Super Mario hüpft von einem Körper zum anderen. Kannst du die Körper benennen und kennst du ihre Definitionen? Notiere dir ihre Namen und vergleiche deine Überlegungen mit der Lösung.
Körper und ihre Definitionen
Heute wollen wir mit Hilfe des Vektorprodukts das Volumen des Spats berechnen. Wenn wir diesen Fall kennen, können wir ihn auch auf andere Fälle übertragen.
Sieh dir dazu das Erklärvideo an und übernimm den Hefteintrag ins Heft.
Erkärvideo
Hefteintrag
Jetzt geht es ans Üben! Wir starten wie immer mit einer Basisaufgabe.
S. 113 Nr. 4
Berechne eine der folgenden Aufgaben. Ist sie falsch, so berechne auch die zweite.

Jetzt kommen wir zu einer weiterführenden Aufgabe.
S. 113 Nr. 5

a) Überprüfe deine Skizze über das GeoGebra-Applet
Kommen wir zu einer Begründe- und Anwendungsaufgabe.
S. 114 Nr. 13

a)
Hinweis: es genügt zu zeigen, dass alle Seiten gleich lang sind und ein rechter Winkel entsteht. So entsteht automatisch ein Quadrat. Berechne hierfür die nötigen Vektoren.
b)
Es reicht, die Längen der Vektoren der vier Seitenkanten zu berechnen.
d)
Bedenke: M ist im Quadrat der Mittelpunkt der Diagonalen.
Und zum Schluss eine Begründeaufgabe.
S. 114 Nr. 14 a, b (c freiwillig: schicke mir zur Korrektur ein Bild deiner Lösung)

Hausaufgaben: S. 114 Nr. 8a, (b freiwillig), 11, 12 und die untenstehende Aufgabe (Verbesserung nächste Stunde)

