Όγκος κύβου και ορθογωνίου παραλληλεπίπεδου
Όγκος κύβου και ορθογωνίου παραλληλεπίπεδου
Αν σας ζητούσαν να περιγράψετε τον όγκο ενός αντικειμένου, πώς θα το κάνατε;
Πώς θα περιγράφατε τις μονάδες με τις οποίες θα τον υπολογίζατε;
Αυτό το κεφάλαιο ασχολείται με τον υπολογισμό του όγκου και τις μονάδες που χρησιμοποιούνται
κατά τον υπολογισμό του όγκου.
Στο τελευταίο κεφάλαιο ασχοληθήκαμε με την περίμετρο, η οποία είναι μια μονοδιάστατη - γραμμική
μέτρηση. Όπως διαπιστώσαμε, η περίμετρος είναι μονοδιάστατη και ουσιαστικά έχει τα χαρακτηριστικά
μιας γραμμής. Ένα καλό παράδειγμα περιμέτρου θα ήταν αν περπατούσατε γύρω (περιμετρικά) από ένα γήπεδο ποδοσφαίρου.
Στη συνέχεια ρίξαμε μια ματιά στο εμβαδό, το οποίο είναι μια δισδιάστατη μέτρηση.
Ένα αντιπροσωπευτικό παράδειγμα είναι η επιφάνεια του τραπεζιού. Αν έπαιρνες
ένα πινέλο να φρεσκάρεις το πάνω μέρος του τραπεζιού, θα έβαφες την περιοχή
της επιφάνειας του τραπεζιού.
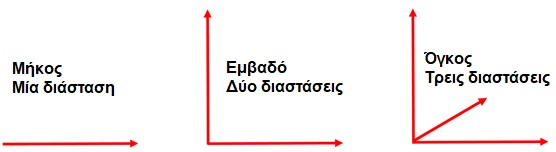
Όταν έχουμε να κάνουμε με τον όγκο, προσθέτουμε μια ακόμη διάσταση, και αυτό καταλήγει να κάνουμε
τρισδιάστατη μέτρηση.
Εδώ είναι μια καλή οπτική αναπαράσταση καθεμίας από τις τρεις διαστάσεις.
Τώρα ας επανεξετάσουμε τις μονάδες μέτρησης. Όταν ασχολούμαστε με γραμμικές μετρήσεις,
αντιμετωπίζουμε τις μονάδες ως έχουν. Δηλαδή μέτρα, εκατοστά και ούτω καθεξής.
Όταν ασχολούμαστε με το εμβαδό, έχουμε να κάνουμε με τετραγωνικές μονάδες όπως τα
τετραγωνικά μέτρα, για να υποδείξουν ότι έχουν δύο διαστάσεις. Για παράδειγμα,
ένα διαμέρισμα μπορεί να έχει επιφάνεια 120 τετραγωνικά μέτρα: 120 m².
Ο τετραγωνισμός των μέτρων υποδεικνύει δύο διαστάσεις, όπως πλάτος και μήκος.
Τώρα όμως προσθέτουμε μια ακόμη διάσταση. Δεν έχουμε μόνο μήκος και πλάτος, αλλά έχουμε
και ύψος - βάθος. Λοιπόν, έχουμε να κάνουμε με κυβικές μονάδες όπως τα
κυβικά μέτρα ή μέτρα3 ή m3 . Το "3" σε αυτή την περίπτωση αντιπροσωπεύει τρεις διαστάσεις
και είναι υπεύθυνο για τον όρο "κυβικό" όταν τον εκφωνούμε. Τώρα είμαστε έτοιμοι να συνεχίσουμε
και να μάθουμε τον τύπο για τον όγκο συγκεκριμένων αντικειμένων.
Όγκος ενός κύβου
Όταν δηλώνεται η λέξη «κύβος», μπορούμε να σκεφτούμε ένα τετράγωνο αλλά απλώς με
μια επιπλέον διάσταση.
Εάν προσθέσετε μια τρίτη διάσταση, θα έχετε όλες τις πιθανές διαστάσεις ίδιες.
Ρίξτε μια ματιά σε έναν από τους πιο διάσημους κύβους στον κόσμο:
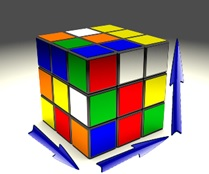
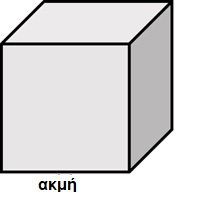
Για να βρούμε τον όγκο του κύβου, πρέπει να πολλαπλασιάσουμε τις τρεις ακμές (διαστάσεις).
Πιο συγκεκριμένα, πολλαπλασιασμό του μήκους, του πλάτους και του ύψους.
Επειδή και οι τρεις ακμές είναι ίδιες, ο τύπος είναι ο ακόλουθος:
Όγκος κύβου=ακμή× ακμή × ακμή
Για να βρείτε τον όγκο ενός κύβου είναι πολύ απλό. Το μόνο που πρέπει να γνωρίζετε είναι
το μήκος της μίας ακμής και έχετε όλες τις πληροφορίες που χρειάζεστε.
Όγκος ορθογώνιου παραλληλεπιπέδου
Ο υπολογισμός του όγκου ενός ορθογώνιου παραλληλεπιπέδου μοιάζει πολύ με τον υπολογισμό του όγκου ενός κύβου εκτός του γεγονότος ότι οι διαστάσεις του είναι όλες διαφορετικές μεταξύ τους.
Όταν ασχοληθήκαμε με ένα ορθογώνιο παραλληλόγραμμο, αναφερθήκαμε στις δύο διαστάσεις
μήκος και πλάτος. Τώρα απλώς προσθέτουμε μια επιπλέον διάσταση που θα ονομάσουμε "ύψος".
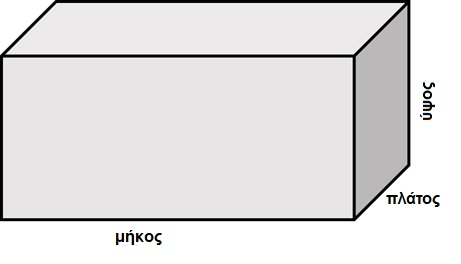
Για άλλη μια φορά, εργαζόμαστε με τρεις διαστάσεις και ο τύπος θα είναι παρόμοιος με αυτόν
ενός κύβου, με τη μεταβλητή "ακμή" να αντικαθίσταται από τις τρεις διαφορετικές διαστάσεις. Τύπος:
Όγκος ορθογωνίου παραλληλεπιπέδου = μήκος × πλάτος × ύψος