Die momentane Änderungsrate
Zu schnell oder noch okay?
Aufgabe 1:
Beschreibe zunächst mit eigenen Worten, was genau in dem Applet abgebildet ist, indem du vollende Fragen beantwortest: Welche Koordinaten hat der Punkt A? Welche Koordinaten hat der Punkt B?
Aufgabe 2:
a) Bestimmen Sie die mittlere Änderungsrate für die erste halbe Stunde der Fahrt. Verschieben Sie dazu die Schieber für und auf die passenden Werte. Geben Sie die mittlere Änderungsrate in das Feld unten ein und überprüfen Sie Ihr Ergebnis.
b) Bestimmen Sie die mittlere Änderungsrate für die zweite halbe Stunde der Fahrt. Verschieben Sie dazu die Schieber für und auf die passenden Werte. Geben Sie die mittlere Änderungsrate in das Feld unten ein und überprüfen Sie Ihr Ergebnis.
c)
Entscheiden Sie, in welche Hälfte der Zeit Paul durchschnittlich schneller gefahren ist.
Zurück zur eigentlichen Frage
Aufgabe 3:
Alex überlegt, wann Paul in dem Zeitraum wohl am schnellsten gewesen ist. Geben Sie den Bereich an, in dem Sie vermuten, dass Paul am schnellsten war.
Hier ist das Applet von oben noch einmal, damit Sie nicht scrollen müssen :)
Aufgabe 4:
Stellen Sie den Schieber für auf =1 und zoomen Sie stark an den Punkt A heran. Untersuchen Sie, wie sich die Sekante verändert, wenn sie mit dem Schieber vergrößern oder verkleinern. Beschreiben Sie Ihre Beobachtungen.
Aufgabe 5:
a) Bestimmen Sie mit dem Applet die Differenzenquotienten für und Tragen Sie die Werte in ihr Heft ein! . Beschreiben Sie, wie sich die Werte verändern.
b) Formulieren Sie eine Schätzung, wie schnell Paul zu diesem Zeitpunkt tatsächlich gefahren sein wird.
Das hier ist ein NEUES Applet, dass den Begriff der Tangente einführt.
Aufgabe 6:
In dem Applet oben wurde eine Gerade mit der Bezeichnung Tangente eingeführt. Erklären Sie kurz was genau diese Tangente sein könnte.
Aufgabe 7:
Nutzen sie die Tangente um die Steigung die Geschwindigkeit von Paul zu dem Zeitpunkt zu bestimmen, an dem er genau eine Stunde gefahren war. Geben Sie die Geschwindigkeit an.
Aufgabe 8:
Suchen Sie unter Verwendung des Applets die Zeitpunkte, an denen Paul exakt 50kmh und 30kmh schnell gefahren ist.
Aufgabe 9:
Ist Paul nach einer Stunde am Ziel angekommen? Begründen Sie unter Verweis auf die Funktion und die Erkenntnisse aus den vorherigen Aufgaben.
Für die Schnellen:
Abb.1.
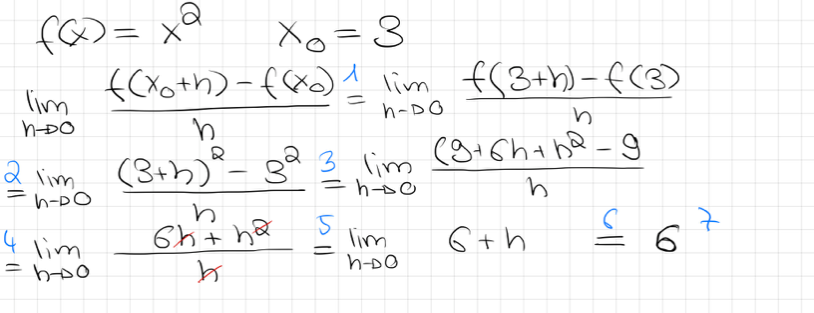
*Aufgabe 10:
In der Abbildung Abb.1. oben wird die momentane Änderungsrate der Funktion mit an der Stelle rechnerisch bestimmt. Versuchen Sie den Rechenweg nachzuvollziehen und zu beschreiben, wie genau in den einzelnen Schritten vorgegangen wird. a) Beschreiben Sie, was in den blau markierten Schritten 1-3 passiert.
b) Beschreiben Sie, was in den blau markierten Schritten 4 und 5 passiert.
c) Beschreiben Sie, was in den blau markierten Schritten 6 und 7 passiert.