Esquema
Cónicas. Historia de su independencia del cono
Las construcciones que componen este libro corresponden a las que aparecen en los distintos capítulos del libro "CÓNICAS. HISTORIA DE SU INDEPENDENCIA DEL CONO" publicado por la Editorial Catarata, el ICMAT y la Federación Española de Sociedades de Profesores de Matemáticas, cuyos auotres son Manuel de León y Agustín Carrillo de Albornoz
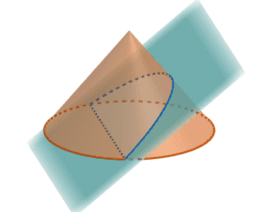
Tabla de contenidos
Las secciones cónicas
- Definición de elipse
- Definición de hipérbola
- Definición de parábola
- Duplicación del cubo
- Lúnula
- Sección del cono
- Punto como sección cónica degenerada
- Recta como sección cónica degenrada
- Dos rectas como secciones cónicas
- Latus rectum en la parábola
- Latus rectum en la hipérbola
- Latus rectum en la elipse
- Círculo de Apolonio
- Problema de Apolonio
Cónicas como lugares geométricos
La importancia de las ecuaciones de las cónicas
Características y propiedades de las distintas cónicas
- Cónicas a partir de su ecuación general
- Excentricidad de la elipse
- Elipse como lugar geométrico - Cuerdas
- Elipse a través de envolventes
- Envolventes para obtener una elipse
- Elipse como lugar geométrico de centros de circunferencias tangentes
- Elipse a partir de las circunferencias principales
- Tangente en un punto de la elipse
- Hipérbola. Definición y elementos
- Hipérbola como lugar geométrico
- Hipérbola como envolvente
- Tangente en un punto de la hipérbola
- Lugar geométrico de puntos que describen una hipérbola
- Definición de parábola
- Construcción de la parábola por puntos
- Parábola a través de envolventes
- Parábola. Propiedad de la tangente
Aplicaciones de las cónicas