aperiodische motieven
aperiodisch
Aperiodische of niet-regelmatige vlakvullingen zijn vlakvullingen waarin je geen verschuivingen kunt vinden die de vlakvulling op zichzelf afbeeldt.
De girih tegels hebben het potentieel om dergelijke vlakvullingen te genereren: 10-voudige symmetrie en een opdelingsregel. Het is duidelijk dat heel wat decoratieve motieven wel regelmatig zijn, ook al maken ze gebruik van vijf- en tienhoeken. In vorige werkbladen van dit boek vind je heel wat voorbeelden van van regelmatige motieven. Maar Lu en Steinhardt verwijzen naar enkele unieke voorbeelden om te illustreren dat de potentie van de girih tegels om dergelijke motieven te creëren ook effectief wordt aangeboord.
opdelingsregel
De tegels in Maragha (1200 nC) worden nog versierd met een tweede, veel vrijer motief dat losstaat van de symmetrieën en vaste snijhoeken van het lijnenpatroon met de giri tegels.
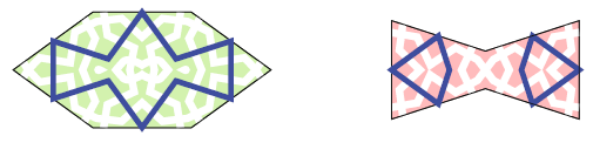
Dit is niet meer het geval in de decoratie van de zwik van de boog van het Darb-e Imamschrijn in Isfahan uit 1453 nC. Hier herken je duidelijk twee decoratielagen, die beide gebaseerd zijn op dezelfde girih tegels.
Van Penrose leerden we dat in een (oneindige) Penrosebetegeling de verhouding van het aantal vliegers t.o.v. het aantal pijlen irrationaal is en het gouden getal benadert. Deze irrationale verhouding is een bewijs van aperiodiciteit.
Ook voor girih tegels kunnen we met wat hogere wiskunde een dergelijke berekening maken. Eerst bepalen we de opdelingsregels voor tienhoek, strik en zeshoek. De eigenschappen van deze transformatie kunnen we weergeven in een matrix. Levert deze matrix irrationale eigenwaarden op, dan heb je een bewijs voor aperiodiciteit.
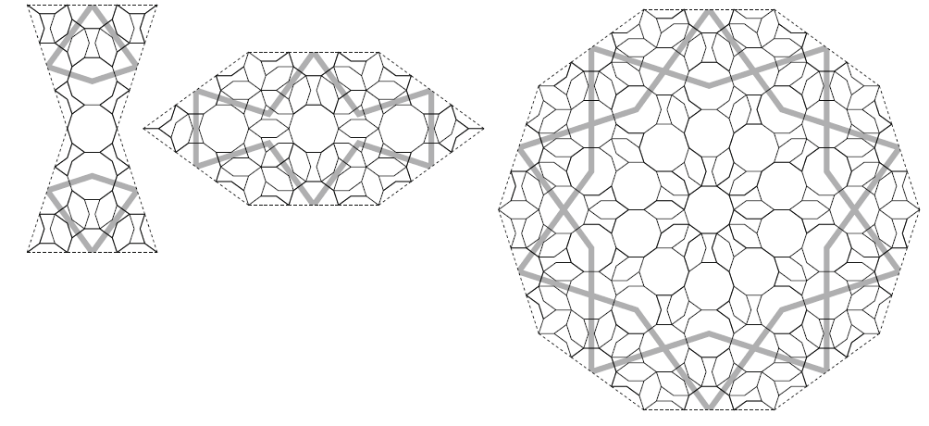
Concreet vonden Lu en Steinhardt bij dergelijke opdelingen dezelfde verhouding terug in de verhouding van zeshoeken en strikken, wat een expliciet bewijs is voor aperiodiciteit. In onderstaande tekening vind je de uitwerking van de opdeling van strik, zeshoek en tienhoek uit het artikel van Cromwell.
geschiedenis heeft zijn rechten en logica heeft zijn regels
Lu en Steinhardt haalden in 2007 het tijdschrift Science en zetten een narratief neer dat online nog steeds vlot wordt gedeeld: "800 geleden kenden ontwerpers van Islamitische geometrische patronen reeds a-periodische patronen op basis van locale 5-voudige symmetrieën die pas in 1974 door Penrose zouden 'ontdekt' worden".
Maar ook voor Lu en Steinhardt becommentarieerden auteurs reeds het vijfvoudige systeem vanuit de bevindingen van Penrose:
- Emil Makovicky schreef in 1992 het artikel "800-year-old pentagonal tiling from Maragha, Iran, and the new varieties of a periodic tiling it inspired."
- Jay Bonner schreef in 2003 het artikel "Traditions of self-similarity".
- "P wist van X en X is een voorbeeld van Y, dus P wist van Y"
- "P wist van X en X impliceert Y, dus P wist van Y".