Kopie von 1) Ähnliche Figuren

Ist Dir das auch schon einmal passiert: Du fügst in einer Präsentation Fotos ein, rückst sie zurecht, bis alles passt, und auf einmal sind die Bilder ganz verzerrt ... wie sieht das denn aus!
Von den Bildern oben haben jeweils zwei die richtigen Proportionen.
Beim Verändern der Größe am Computer kannst Du das in den meisten Anwendungen vermeiden, indem Du die Umschalt-Taste während des Veränderns gedrückt hältst und/oder nur an den Ecken ziehst.
Aber was macht das "richtige" Bild denn eigentlich aus? Es ist doch auf allen Bildern das Gleiche drauf.
Wenn Original und verändertes Bild gleich aussehen, gilt:
Umgangssprachlich formuliert:
Figuren, die exakt die gleiche Form haben, heißen zueinander ähnlich.
Sind die Figuren auch gleich groß, heißen sie zueinander kongruent.
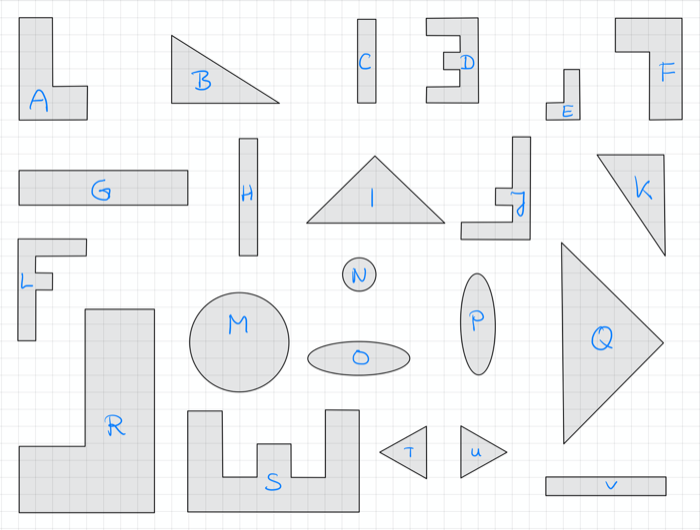
Notiere die Paare der zueinander ähnlichen Figuren und vergleiche:
Notiere die Paare der zueinander kongruenten Figuren und vergleiche:
Bedingungen für Kongruenz und Ähnlichkeit
Wir beschränken uns auf die Betrachtung von Dreiecken.
1) Kongruenz:
Dreiecke sind kongruent, wenn alle drei Seiten gleich lang sind. Damit sind auch automatisch alle drei Winkel gleich groß. Es reicht, drei bestimmte Größen zu kennen, um die Kongruenz von Dreiecken festzustellen. Vergleiche hierzu die Kongruenzsätze sss, wsw, ssw und sws.
2) Ähnlichkeit:
Ähnliche Figuren haben "die gleiche Form", also sind alle Winkel in den Figuren gleich. Die Längen ändern sich mit dem gleichen Faktor. Für Dreiecke gilt also:
Wenn zwei Dreiecke in zwei* Winkeln übereinstimmen, sind sie zueinander ähnlich.
*automatisch ist dann auch der dritte Winkel gleich.
