Ітеративні побудови на базі послідовності точок кола
Наступна побудова з використанням послідовностей лежить в області математичного мистецтва.
Математичного – тому що воно дозволить наочно досліджувати алгебраїчну криву
кардіоїду; мистецтва – тому що її побудова несе певну естетичну красу.
Нагадаємо, що кардіоїда – це пласка лінія, алгебраїчна крива четвертого порядку, яка отримала свою
назву через схожість своїх обрисів зі стилізованим зображенням серця. Має один
касп – своєрідну вершину. Геометрично описується фіксованою точкою кола, що
котиться по нерухомому колу з таким же радіусом. Побудова цим способом описується
в розділі «Епіциклоїди».
В попередньому підрозділі описувався поділ відрізка на рівні частини за допомогою
послідовності точок. У цій побудові ділити потрібно коло.
Задача на побудову 1. Реалізувати інтерактивну побудову на базі послідовності точок кола для одержання кардіоїди.
Навчальне дослідження 1. Самостійно розберіть і опишіть дію наведеної нижче
формули послідовності. CirclePoints –
такий же список точок, як у кардіоїди, відрізок СВ – діаметр «кола» точок. Побудуйте дану послідовність і зробіть висновки про результуючу конструкцію.
Послідовність[Коло[Елемент[CirclePoints, k],
Перетин[Перпендикуляр[Елемент[CirclePoints, k], Відрізок[С, B]],Відрізок[С, B]]], k, 1, n]
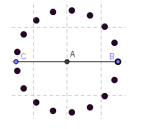
Відповідь
Навчальне дослідження 1:
Перетин[Перпендикуляр[Елемент[CirclePoints, k], Відрізок[С, B]],
Відрізок[С, B]] – визначає перетин
відрізка СВ і опущеного на нього перпендикуляра з поточної точки списку CirclePoints.
В результаті виконання послідовності створюється список кіл, центрами яких є
точки зі списку CirclePoints, причому кожне коло проходить через описану вище
точку перетину перпендикуляра і відрізка СВ (тобто, є дотичною до нього).
Огинаюча крива даного списку кіл утворює алгебраїчну криву шостого порядку нефроїду,
яка також є окремим випадком епіциклоїди.
