Wiederholung: Quadratische Gleichungen
Heute gibt es eine Wiederholung zu quadratischen Gleichungen. Das Lösen dieser Gleichungen bildet die absolute Grundlage für den Umgang mit Polynomfunktionen. Lies dir im hier noch einmal die Wiederholung zu quadratischen Gleichungen durch und löse dann die Aufgaben.
Erinnerung:
Eine quadratische Gleichung hat die allgemeine Form:
Arten der quadratischen Gleichung:
Normalform: Um auf die Normalform zu kommen, teilt man einfach durch a.
Quadratische Gleichung ohne konstantes Glied:
Natürlich kannst du alles mit dem Hau-drauf-Werkzeug "Mitternachtsformel" lösen. Nicht immer ist das aber der einfachste Weg.
Reinquadratische Form:
zur quadratischen Gleichung ohne konstantes Glied
zur reinquadratischen Gleichung
Dazu gibt es noch Sonderfälle, die man ohne die Mitternachtsformel viel schneller lösen kann. Einer davon wäre:
Faktorisierte Form:
Hier musst du nichts ausmultiplizieren. Viel einfacher geht es mit diesem Satz:
Ein Produkt ist Null, wenn mindestens ein Faktor gleich Null ist.
Du suchst also den Wert für x, für den die Klammer Null wird.
Beispiel:
Binomform:
Auch bei diesen Gleichungen ist die Mitternachtsformel "zu viel Arbeit".
Beispiele
|
|
|
(Betragsschreibweise)
Übrigens könntest du das auch per Substitution lösen.
Wir wollen herausfinden, was in der Klammer stehen muss. Also setzen wir und lösen die Gleichung . Lösen wir es auf, erhalten wir . Dann wird rücksubstituiert:
.
Die Unterteilung in die verschiedenen Gleichungsarten ist sehr rezepthaft. Vieles davon machst du wahrscheinlich schon ganz intuitiv so.
Tust du dich aber schwer, welches Lösungsverfahren angewandt werden soll, kannst du hier Hilfe finden.
Hier ein paar eher einfache Übungen. Entscheide hier selbst, was das beste Lösungsverfahren ist. Alle diese Aufgaben lassen sich locker im Kopf rechnen. Übe das hier doch gleich einmal.
Aufgabe 1
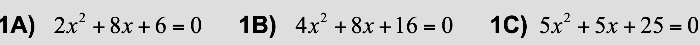
Lösung
Aufgabe 2
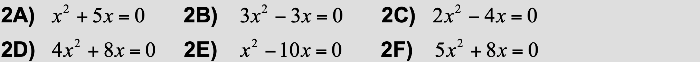
Lösung
Übung 3
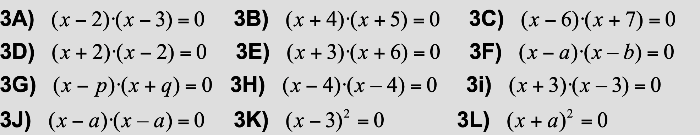
Lösung
![Das geht[b] locker[/b] im Kopf.](https://www.geogebra.org/resource/khnwtfqb/F41q8oQ8mtq5KmUt/material-khnwtfqb.png)
Lösung

Lösung
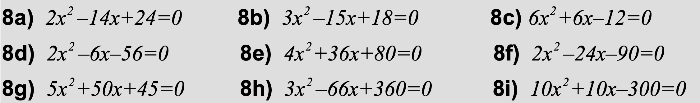
Lösung