Addition und Zerlegung von Kräften
Wiederholung: Graphische Addition und Zerlegung von Vektoren
Zum Verständnis des nachfolgenden Kapitels benötigen wir etwas mathematisches Rüstzeug. Wir wiederholen daher die graphische Additon und die Zerlegung von Vektoren.
Wiederholung: Graphische Vektoraddition
Wiederholung: Graphische Vektorzerlegung
Kräftezerlegung: Gezogener Waggon
Kräftezerlegung: Ziehen eines Wagens
Wenn du einen Wagen oder eine Rodel ziehen musst, wird dir vielleicht aufgefallen sein, dass eine zu kurze Deichsel (oder eine zu kurze Leine) das ziehen merklich erschwert. Anstatt den Wagen zu ziehen, verschwendest du einen Teil der Kraft, um den Wagen in die Höhe zu heben.
Die Zugkraft wird in zwei Komponenten aufgespalten:
- Die Hubkomponente FHub hebt den Wagen in die Höhe. Sie zeigt nach oben.
- Die Zugkomponente FZug zieht tatsächlich den Wagen. Sie zeigt nach vorn.
Rechenbeispiel: Zug- und Hubkomponente
Wir betrachten einen Fall, in dem die Muskelkraft F in einem 30° Winkel zur Horizontalen angreift.
Wir nehmen an, dass die Kraft F=600 N beträgt.
Skizze:
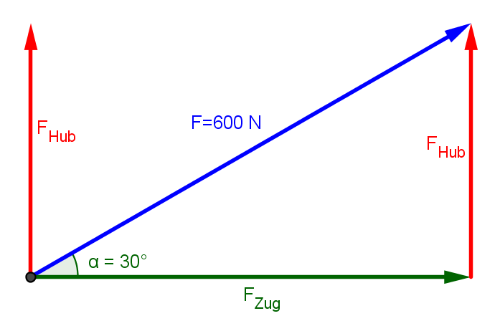Wie groß sind Zug- und Hubkomponente unter diesen Bedingungen?
Wie groß sind Zug- und Hubkomponente unter diesen Bedingungen?Zug- und Hubkomponente - Lösung
Im Grunde spricht nichts dagegen, die Lösung einfach zu finden, indem man das oben skizzierte Dreieck möglichst genau zeichnet und die Lösung (d.h die Länge der beiden kürzeren Seiten) abliest.
Wir zeigen die rechnerische Lösung.
Wir können den Umstand ausnützen, dass die Richtungen der beiden Kräfte normal auf einander stehen ("Nach oben" steht normal auf "nach vorne").
Deswegen gilt:
Damit also:
Man erhält FHub=300 N.
Für die Zugkomponente erhält man in ähnlicher Weise:
Damit also:
Man erhält FZug=519,62 N.
Eine Zeichnung führt dich (möglicherweise sogar schneller) zum gleichen Ergebnis.
Vektoriell gilt:
Es gilt daher:
Die beiden Komponenten addieren sich also zur Gesamtkraft F.
Kräftezerlegung: Seilbahn
Tragseil einer Seilbahn
Eine Seilbahn übt eine Kraft von 150.000N auf einer horizontalen Ebene aus.
Der Seilwinkel beträgt 10° zur Horizontalen.
Welche Kraft muss das Tragseil der Seilbahn aushalten?
Löse rechnerisch oder graphisch, oder verwende das Applet!
Aufgabe: Aufhängung eines Schildes
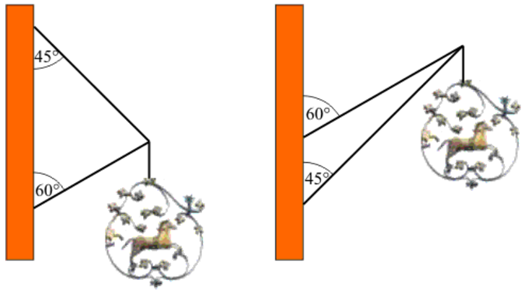
Ein Gasthaus will ein Schild aufhängen.
Die Abbildungen zeigen zwei verschiedene Tragekonstruktionen für ein Wirtshausschild, welches
die Gewichtskraft 200 N besitzt.
Ermittle durch eine genaue Zeichnung oder Rechnung (Vorlage auf deinem Arbeitsblatt) die Kräfte in den Stäben der Tragekonstruktion.
Welche der beiden Möglichkeiten würdest du empfehlen?