Jäävad ja muutuvad suurused. Funktsiooni mõiste
1. Jäävad ja muutuvad suurused
Igapäevaelus me mitte ainult ei märka, vaid ka kasutame erinevaid suurusi (väärtusele viitaja), millest ühed on muutuvad suurused (muutuvad protsessi käigus), teised aga jäävad suurused (protsessi käigus ei muutu). Jäävad suurused ehk konstandid on näiteks
- täispöörde suurus ;
- ööpäeva pikkus 24 h;
- ringjoone pikkuse ja diameetri suhe ;
- maa ekvaatori pikkus jne.
- kaupade hind;
- auto liikumiskiirus;
- inimese vanus, pikkus, kaal;
- maapinnale langev sademete hulk jne.
2. Funktsioon
Mõtleme mingisugusele masinale, millel on kindel ülesanne, mida täita, näiteks snäkiautomaadile. Snäkiautomaadi ülesanne ehk funktsioon on raha sisestamisel väljastada kliendile soovitud kaup (nt suupisted, kommid, karastusjoogid jne). Seega võime mõelda masinast kui funktsioonist, mis neelab metallraha (sisend), valib kliendi poolt soovitud toote nt karastusjoogi ja väljastab selle (väljund).
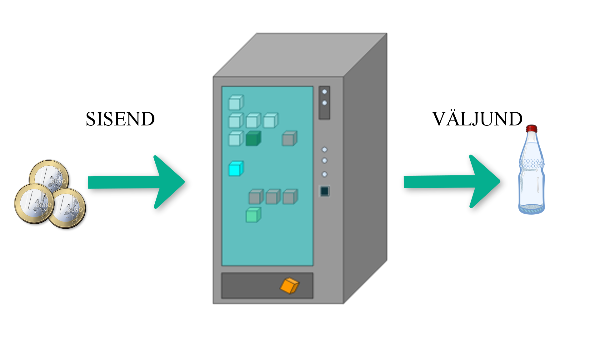
Seega karastusjoogi saamine sõltub väljastamisele eelnevast protsessist. Järgnevalt püüame funktsiooni käsitleda rohkem matemaatilisest vaatenurgast. Kuidas sõltumatud ja sõltuvad muutujad on omavahel seoses? Vaata alljärgnevast videost ja saad teada (NB! Veendu, et subtiitrid oleksid sisse lülitatud).
Vaadeldes funktsiooni teatud tüüpi masina ülesandena, annab piltliku ettekujutuse, mis on funktsioon. Siiski matemaatilises keeles vajame täpsemat sõnastust funktsioonile. Funktsiooniks nimetatakse eeskirja, mis seab sõltumatu muutuja igale väärtusele vastavusse sõltuva muutuja mingi ühe kindla väärtuse. Sõltumatut muutujat nimetatakse funktsiooni argumendiks (tähistatakse tavaliselt ), argumendi väärtuse järgi leitud sõltuva muutuja vastavaid väärtusi nimetatakse funktsiooni väärtusteks (tähistatakse tavaliselt ). Asjaolu, et üks muutuja on teise funktsioon tähistatakse ja loetakse: on -i funktsioon.
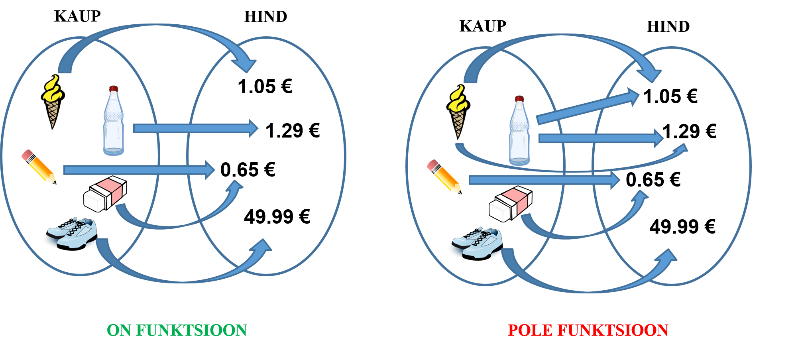
Funktsiooni mõiste ei nõua, et igale -i väärtusele vastaks ainult üks -i väärtus. Näiteks ühesugune hind ühes ja samas poes võib olla mitmel erineval kaubal. See-eest peab aga igale -i väärtusele vastama üks ja ainult üks -i väärtus. Näiteks ühel ja samal kaubal ühes ja samas poes ei saa olla korraga mitu erinevat hinda. Seega on oluline meelde jätta, et iga argumendi väärtusele vastab parajasti üks funktsiooni väärtus.
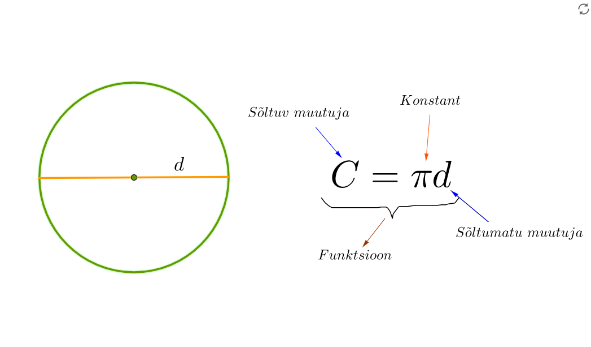
Näiteks ringjoone pikkuse sõltuvust diameetrist kirjeldab funktsioon. Ringjoone pikkus on ringjoone diameetri funktsioon, sest diameetri igale pikkusele (argumendi väärtusele) vastab valemi põhjal kindel ringjoone pikkus (funktsiooni väärtus).
3. Funktsiooni esitusviisid
Funktsioone saab esitada mitmel viisil:
1) valemina;
2) tabelina (mis koostatakse muutujate omavahelise seose e. valemi järgi);

3) graafikuna (mis saadakse tabeli abil);
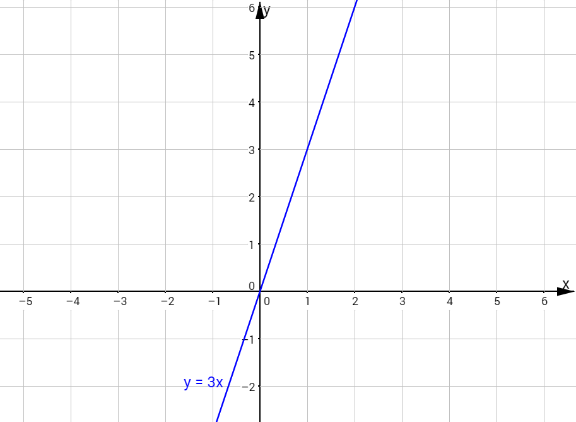
4) diagrammina (näiteks sektordiagrammina, kus funktsiooni väärtusteks on protsendid);
5) sõnaliselt
Näide 1. Ruudu ümbermõõt sõltub ruudu külje pikkusest st ruudu ümbermõõt on ruudu külje funktsioon.
Näide 2. Ringjoone pikkus sõltub ringjoone diameetrist st ringjoone pikkus on diameetri funktsioon.
4. Lihtsamaid näiteid funktsioonidest/mittefunktsioonidest
1) Kuubi ruumala on kuubi serva funktsioon, sest serva igale pikkusele (argumendi väärtusele) vastab valemi põhjal kindel kuubi ruumala (funktsiooni väärtus).
2) Telefonikõne maksumus , kui kõneminuti hind on nt 0,22 eurot, on kõne pikkuse funktsioon, sest kõne igale kestvusele (argumendi väärtusele) vastab valemi põhjal kindel telefonikõne maksumus (funktsiooni väärtus).
3) Kui taksosõidu alustamistasu on 2 eurot ja iga kilomeetri eest tuleb tasuda 0,5 eurot, siis seos sõidu hinna ja läbitud kilomeetrite vahel väljendub valemina. See seos on funktsioon, mille puhul saab leida läbitud kilomeetrite arvu (argumendi) iga väärtuse järgi ühe kindla sõidu maksumuse (funktsiooni väärtuse).
4) Seos inimese massi ja tema vanuse vahel pole funktsioon, sest inimese mass oleneb veel paljudest, täpsemalt mittemääravatest juhuslikest teguritest. Seetõttu pole võimalik leida nt, kui suur mass vastab inimese 30. eluaastale.