Das Bogenmaß
Wiederholung - Sinus und Kosinus am rechtwinkligen Dreieck
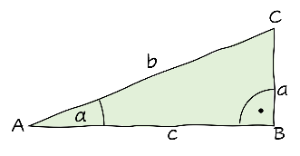
Kreuze zum gegebenen Dreieck die richtigen Beziehungen an.
Wiederholung - Sinus und Kosinus am Einheitskreis
Gib mithilfe des Einheitskreises gerundete Werte für und an.
Erinnerung:
Der Sinuswert des Winkels entspricht der y-Koordinate des Punkts P auf dem Einheitskreis (Radius 1).
Der Kosinuswert entspricht der x-Koordinate von P.
Bogenmaß
Man kann sagen, dass Mathematiker eine gewisse Abneigung gegenüber Einheiten hegen. Aus diesem Grund werden wir uns heute vom Gradmaß (°) verabschieden und eine neue Methode der Winkelmessung kennen lernen.
Betrachte dazu das folgende Applet und erkläre, wie die Bogenlänge b mit dem Winkel zusammenhängt.
Tipp zum Vorgehen: Berechne erst die Bogenlänge b für , dann für und für .
Berechne die Bogenlänge b für den Winkel .
Wir können jedem Winkel somit eine Bogenlänge b im Einheitskreis zuordnen. Dementsprechend können wir anstelle der Angabe eines Winkels auch die Angabe einer Bogenlänge verwenden. Ein Winkel von entspricht beispielsweise dem Winkel 90°.
| Merke: Wird ein Winkel im Bogenmaß gegeben, wird er meist mit x bezeichnet. Wird dagegen Gradmaß verwendet nehmen wir griechische Buchstaben. |
Bestimme nun mit dem Einheitskreis wieder die gerundeten Werte für Sinus und Kosinus.
Tipp zum Vorgehen: Nutze den Dreisatz. Ein Winkel von 360° entspricht . Ein Winkel von 70° entspricht daher .
Erkläre die Rechnung im Tipp:
Hefteintrag
Übertrage nun den Hefteintrag in dein Heft:
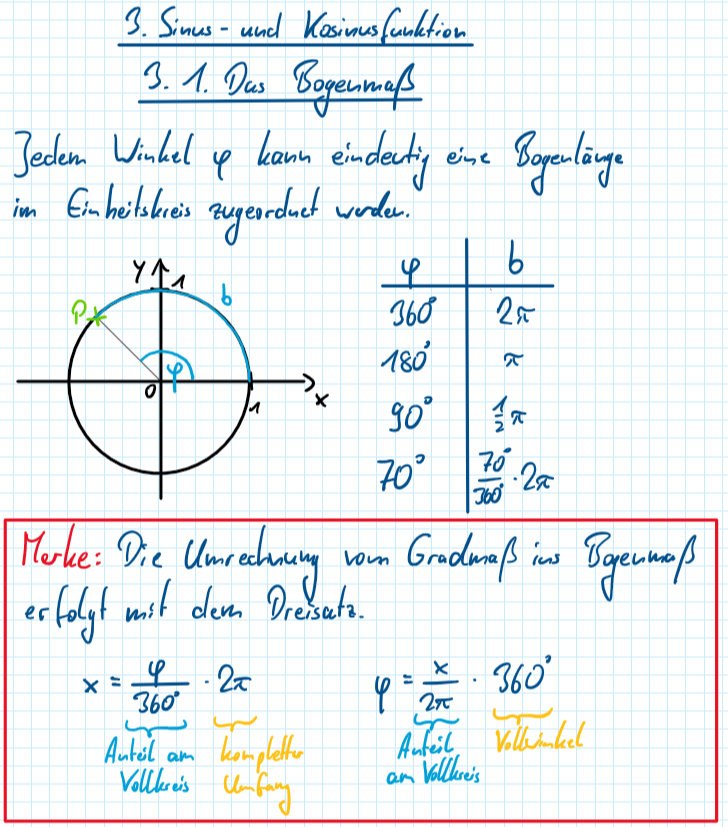
Übung
Bearbeite nun die Aufgaben S. 70/1 a - d und S. 71/2 a - d.