Determinants

Author:Emily_Gabriel1, Brian Sterr, Pratima Nayak, Fanie Lychouna, Hisham Amir

Warm Up!

Simplify the following matrix:

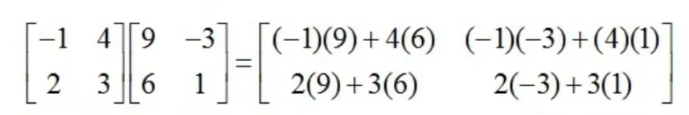
Write the final answer in matrix form. (Use M={{_,_},{_,_}})

What is a determinant?

The determinant of a square matrix is a single value, which is computed from the elements of that square matrix. The determinant can be used to solve a system of linear equations, perform mathematical operations, and find the area or volume of geometric shapes

Notation

A determinant can be written in two ways: det A or |A|

To calculate the determinant refer to the picture below:

Try it on your own!

Use the applet below to practice finding the determinant! (Press check answer after you have inputed a value for the determinate in the red box.)

Looking at determinants geometrically

We can use determinants to find the area of geometric shapes.

The applet below shows the connection between the determinant of a 2x2 matrix and the parallelogram. The determinate is the area of the parallelogram defined by the two vectors. You can change the two vectors being used by either dragging their heads or by typing in coordinates for the head. Interact with the applet below to help answer the following questions.

What do you notice about the area of the parallelogram and the determinant of the 2x2 matrix?

What happens to the determinant when you switch the position of and so that the angle from the positive -axis to is smaller than that of ?

Select all that apply

A
The determinant is positive
B
The determinant is negative

Check my answer (3)

What is the relationship between the components of and the components of in terms of the elements in the corresponding matrix?

Select all that apply

A
The first row represents the x values and the second row represents the y values.
B
The first row represents the y values and the second row represents the x values.
C
The first column represents the x values and the second column represents the y values.
D
The first column represents the y values and the second column represents the x values.

Check my answer (3)

Your turn!

Interact with the applet below to choose two different positions for the two vectors. Then, find the determinant.

Write the two cartesian points you used and the determinant.

Looking at determinants algebraically

Cramer's Rule is a method that uses determinants to solve systems of linear equations that have the same number of equations as variables. Cramer's rule is used to solve for a variable without solving every single equation.

Note: If we are solving for

, the

column is replaced with the constant column. If we are solving for

, the

column is replaced with the constant column.

Let's look at an example!

Use the applet below to move the sliders to the correct values to get: equation 1:

equation 2:

Then, click on the boxes to get a step by step guide on systems of linear equations using Cramer's Rule.

What do you get for your x and y values for the system? equation 1: equation 2:

Now, interact with the applet again to change the coefficients of equation 1 and 2 until you get an infinite solution. What were the equations? What do you notice about the equations?

Can you find an equation where you change the coefficients of equation 1 and 2 to get no solution? What was the equation? What do you notice about the equation?