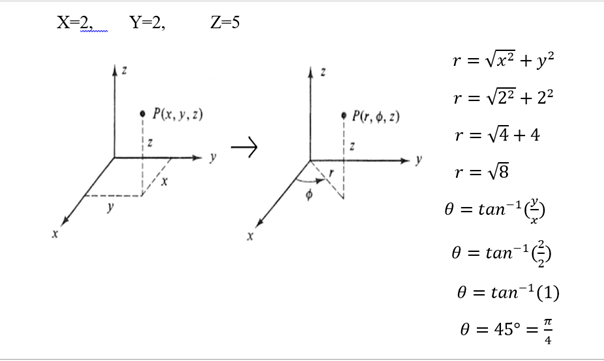
Transformación de coordenadas cilíndricas a cartesianas y viceversa
Las coordenadas cartesianas tridimensionales permanecen representadas en la manera (x, y, z). Un sistema de coordenadas tridimensional alterno es el sistema de coordenadas cilíndricas. El sistema de coordenadas cilíndricas es una expansión en 3 magnitudes del sistema de coordenadas polares. Las coordenadas polares son extendidas en la tercera magnitud parecido a como extendimos a las coordenadas cartesianas, o sea,
sencillamente agregamos a z como la tercera magnitud. Entonces, las coordenadas cilíndricas poseen la manera (r, θ, z), en donde, r es la distancia a partir de los principios hasta la postura del punto en el plano xy, θ es el ángulo con respecto al eje x y z es la coordenada en el eje z.
1. Tenemos al punto (3, 30°, 6) en coordenadas cilíndricas. ¿Cuál es su equivalencia en coordenadas cartesianas?
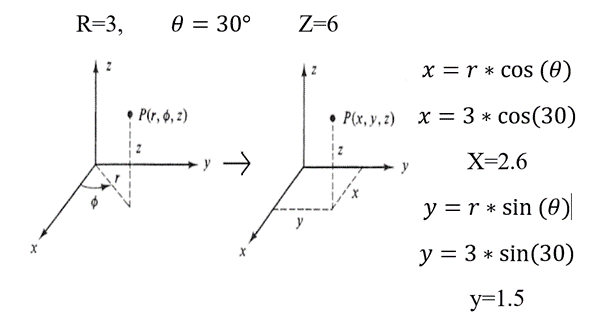
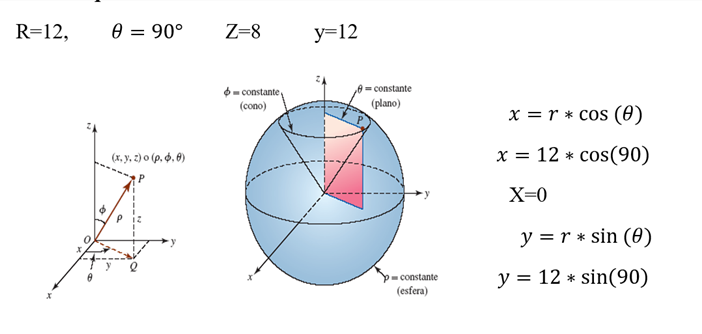
2. Tenemos al punto (12, 90°, 8) en coordenadas cilíndricas. ¿Cuál es su equivalencia en coordenadas cartesianas?
3. Si es que tenemos las coordenadas cartesianas (2, 2, 5), ¿Cuál es la equivalencia en coordenadas cilíndricas?