"Spherical Coordinates to 3D Coordinates"
3D - Space
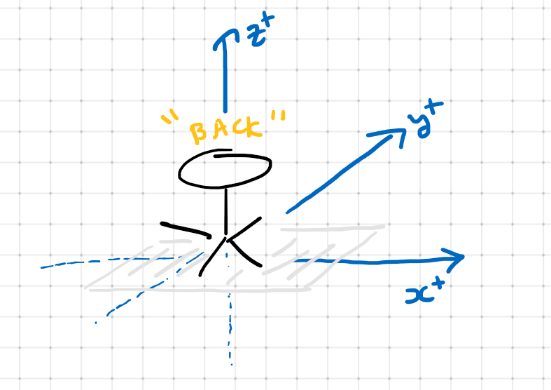
Standing anywhere in your room, you can define 3 positive directions : (1) walking to the right, (2) walk forward and (3) going toward the sky.
We say then that our world is three - dimensional or 3D because, where ever we need to go, we can get there using the three directions above.
The x - coordinate or x direction is walking right or left, the y - coordinate or y direction is moving forward and backward, and the z direction is, moving either up or down.
3D Plotting
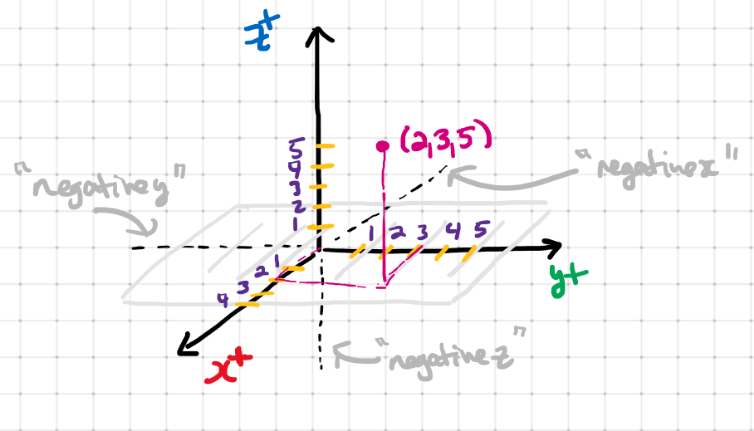
We we'll draw our three axis like below and plot points as indicated.
Exercise 1
Plot the points (1,2,1) and (2,2,2) below.
Remember : The command A = (a,b,c) plots the point (a,b,c).
Red = x - axis, Green = y - axis and Blue = z - axis.
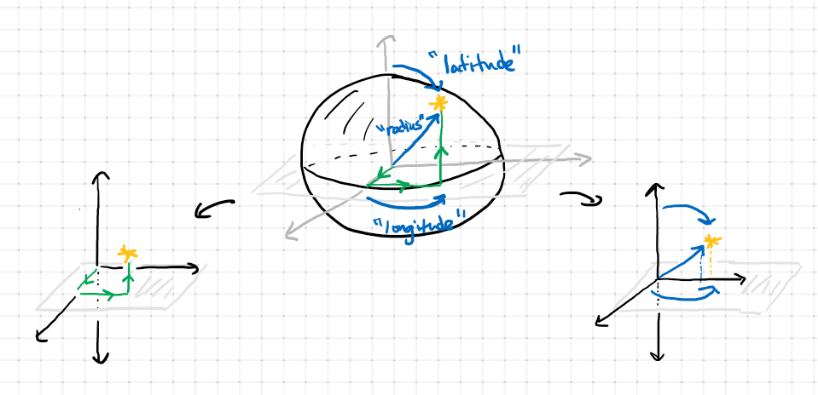
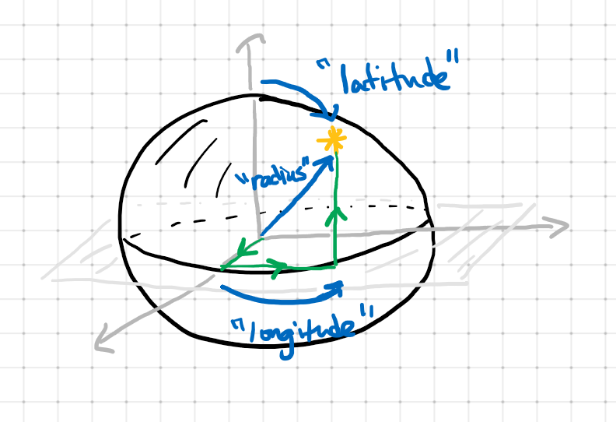
Spherical Coordinates
The coordinates of a sphere are given by latitude, longitude and radius (check the image above). The latitude and longitude is given in degrees and radius is in the units you are using for distance, so inches, feet, miles, etc.
Therefore, unlike in 3D coordinates, the coordinates on a sphere are (latitude, longitude, radius). However, there's a relation between the two. There are some functions called cosine = cos and sine = sin which allow us to say,
If an object is at the coordinate (latitude, longitude, radius) on a sphere, then the corresponding (x,y,z) coordinates in 3D are give by,
x = radius * cos(longitude) * sin(latitude)
y = radius * sin(longitude) * cos(latitude)
z = radius * cos(latitude)
Exercise 2
Air Marshall Beans McGoogle is trying to mount a base below a flying object. He gives you the objects coordinates as (60 degrees, 30 degrees, 2miles).
Part I
Compute the corresponding (x,y,z) coordinates using the calculator below.
Calculator. Use "deg" for degrees.
Part II
What are the (x,y,z) for the above?