Babylonian Method of Extraction of Square Root
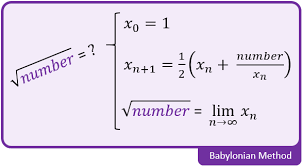
The Babylonian square-root algorithm. The iterative method is called the Babylonian method for finding square roots, or sometimes Hero's method. It was known to the ancient Babylonians (1500 BC) and Greeks (100 AD) long before Newton invented his general procedure. Here's how it works. Suppose you are given any positive number S. To find the square root of S, do the following:
- Make an initial guess. Guess any positive number x0.
- Improve the guess. Apply the formula x1 = (x0 + S / x0) / 2. The number x1 is a better approximation to sqrt(S).
- Iterate until convergence. Apply the formula xn+1 = (xn + S / xn) / 2 until the process converges. Convergence is achieved when the digits of xn+1 and xn agree to as many decimal places as you desire.
- An initial guess is x0 = 10.
- Apply the formula: x1 = (10 + 20/10)/2 = 6. The number 6 is a better approximation to sqrt(20).
- Apply the formula again to obtain x2 = (6 + 20/6)/2 = 4.66667. The next iterations are x3 = 4.47619 and x4 = 4.47214.