Krümmungsverhalten einer Exponentialfunktion - Didaktischer Kommentar
Kurzbeschreibung
Diese Aktivität kann relativ frühzeitig nach dem Erarbeitungsprozess von Exponentialfunktionen eingesetzt werden, da nur Grundlagen gefordert sind. Es geht um das Erkennen einer einfachen Exponentialfunktion samt zugehörigen Funktionsgraphen. Das Krümmungsverhalten können die Schülerinnen und Schüler sogar vom Funktionsgraphen ablesen. Diese Aufgabe eignet sich auch sehr gut zum Austeilen auf einem Blatt Papier, da keine dynamischen Aktivitäten gefordert sind.
Kompetenzen
Die Schülerinnen und Schüler können ...
- exponentielle Zusammenhänge graphisch angegeben als Exponentialfunktion erkennen.
- exponentielle Zusammenhänge durch eine Formel angeführt als Exponentialfunktion deuten.
- zwischen den eben genannten unterschiedlichen Darstellungsformen dieser exponentiellen Zusammenhänge wechseln.
- mithilfe der angegebenen Funktionsgleichung Wertepaare ermitteln und mithilfe deren den Kontext deuten.
- den Funktionsgraphen als links- oder rechtsgekrümmt interpretieren.
Kopiervorlage für Schülerinnen und Schüler
Lösungen
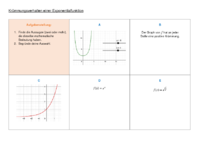
- Bei Aussage D handelt es sich um die Zielaussage in Form einer Funktionsgleichung.
- Aussage C teilt dieselbe Bedeutung wie die Zielaussage D, da es sich hier lediglich um eine andere Darstellungs- bzw. Repräsentationsform der gegebenen Funktion handelt, explizit um den Graphen der beschriebenen Exponentialfunktion.
- Aussage B teilt ebenfalls dieselbe Bedeutung wie die Zielaussage D und beschreibt eine Eigenschaft der Zielaussage D - wieder handelt es sich nur um eine andere Darstellungs- bzw. Repräsentationsform.
- Aussage E hat nicht dieselbe mathematische Bedeutung wie die Zielaussage D, da die Art der Exponentialfunktion verändert wurde - aber Aussage E erscheint in derselben Darstellungs- bzw. Repräsentationsform wie D.
- Aussage A hat nicht dieselbe mathematische Bedeutung wie die Zielaussage D (es handelt sich um einen beliebigen Graphen) und verwendet nicht dieselbe Darstellungs- bzw. Repräsentationsform wie die Zielaussage D, da hier eine andere Art von Zeichensystem verwendet wird.