Hypozykloide
Definition
Kurve, die ein Peripheriepunkt eines Kreises beschreibt, wenn dieser Kreis auf der inneren Seite eines anderen, festen Kreises abrollt.
![[size=150]Den Kreis kann man auch in einem anderen Kreis abrollen lassen. Man
erhält nun eine Hypozykloide. Eine solche entsteht zum Beispiel, wenn man mit einem
Spirographen ein Mandala zeichnet.[/size]](https://www.geogebra.org/resource/dzhhcr4b/kMwPvyQNTQvF5d1U/material-dzhhcr4b.png)
Verschlungene Hypotrochoide
Die Anzahl an Schleifen während einer Periode ist identisch mit der Zahl iZ und somit identisch mit der Anzahl an Spitzen der Zykloide.
Verschlungene Trochoiden weisen mindestens iZ Schnittpunkte mehr als die (gespitzte) Zykloide auf. Die genaue Anzahl an Schnittpunkten lässt sich nur ermitteln mit Hilfe von Übergangskurvenpunkten. Ein Übergangskurvenpunkt erzeugt eine Trochoide mit Berührungspunkten. Die Anzahl an Übergangskurvenpunkten und somit an Trochoiden mit Berührungspunkten ist gleich dem Integerwert von {\displaystyle (i_{Z}/2)}
. Somit treten keine Berührungspunkte auf, wenn iZ gleich 1 ist.
Leider lassen sich Übergangskurvenpunkte nicht analytisch berechnen. Die Ermittlung mit Hilfe von Näherungsverfahren ist nicht kompliziert, würde aber den Rahmen dieses Artikels sprengen. Daher sollen hier nur die Phänomene zur Erzeugung der Formenvielfalt der verschlungenen Trochoiden erläutert werden. Die Formen und deren Vielfalt ist so faszinierend, dass diese Faszination von einem speziellen Spielzeug genutzt wird, nämlich dem Spirograph. Mit einem Spirograph können manuell verschiedene blumig anmutende verschlungene Hypotrochoiden mit Hilfe von Bleichtiften erzeugt werden. Die Bleistifte werden durch Löcher eines in einem Hohlrad umlaufen Zahnrades gesteckt und so lang über ein Papier geführt, bis sich eine geschlossene Kurve ergibt.
Das durch geringe Variation des Abstandes des Loches zum Mittelpunkt des umlaufenden Rades immer wieder anders anmutende Hypotrochoiden entstehen, lässt sich anhand der Sonderfälle erläutern, bei denen Trochoiden mit Berührungspunkten entstehen.
. Somit treten keine Berührungspunkte auf, wenn iZ gleich 1 ist.
Leider lassen sich Übergangskurvenpunkte nicht analytisch berechnen. Die Ermittlung mit Hilfe von Näherungsverfahren ist nicht kompliziert, würde aber den Rahmen dieses Artikels sprengen. Daher sollen hier nur die Phänomene zur Erzeugung der Formenvielfalt der verschlungenen Trochoiden erläutert werden. Die Formen und deren Vielfalt ist so faszinierend, dass diese Faszination von einem speziellen Spielzeug genutzt wird, nämlich dem Spirograph. Mit einem Spirograph können manuell verschiedene blumig anmutende verschlungene Hypotrochoiden mit Hilfe von Bleichtiften erzeugt werden. Die Bleistifte werden durch Löcher eines in einem Hohlrad umlaufen Zahnrades gesteckt und so lang über ein Papier geführt, bis sich eine geschlossene Kurve ergibt.
Das durch geringe Variation des Abstandes des Loches zum Mittelpunkt des umlaufenden Rades immer wieder anders anmutende Hypotrochoiden entstehen, lässt sich anhand der Sonderfälle erläutern, bei denen Trochoiden mit Berührungspunkten entstehen.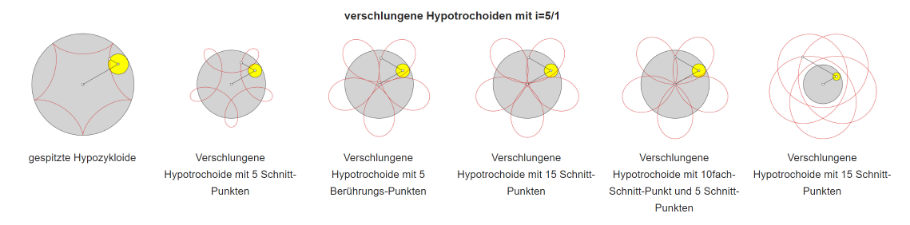
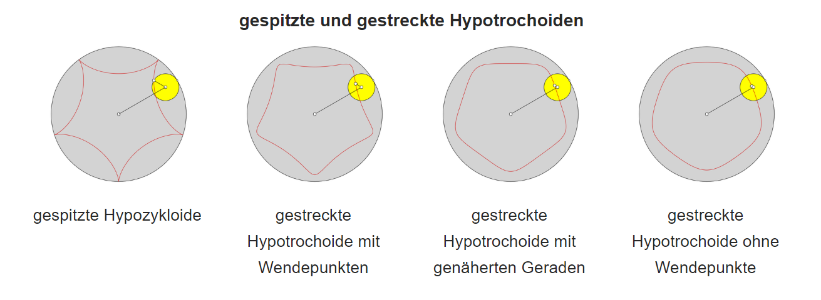
Gestreckte Epi-, Peri- und Hypotrochoide
GAlle gestreckten Hypotrochoiden weisen die gleiche Anzahl an Schnittpunkten auf wie die gespitzten, also s0.
Die gestreckten Trochoiden lassen sich unterscheiden in Trochoiden mit Wendepunkten und ohne.
- Der Krümmungsmittelpunkt von Trochoiden mit Wendepunkten wechselt in jedem Wendepunkt von einer Seite der Kurve auf die andere. Somit weisen diese Trochoiden Links- und Rechtskurven auf. Die Anzahl der Links- wie auch der Rechtskurven ist iZ und damit gleich der Anzahl der Spitzen. Die Anzahl der Wendepunkte ist somit 2*iz. Punkte, die gestreckte Trochoiden mit Wendepunkten erzeugen, liegen in der Nähe des Randes des umlaufenden Rades.
- Punkte, die gestreckte Trochoiden ohne Wendepunkte erzeugen, liegen weiter entfernt vom Rand des umlaufenden Rades.
- Getrennt werden beide Bereiche durch den Sonderfall, dass die gestreckten Trochoiden eine genäherte Gerade durchlaufen. Dies ist der Fall, wenn der erzeugende Punkt auf der BALLschen Kurve liegt und somit folgenden Abstand rB zum Mittelpunkt des umlaufenden Rades aufweist: rb=rg/(1+iz/in) Die Anzahl der genäherten Geradenist gleich iZ und damit gleich der Anzahl an Spitzen
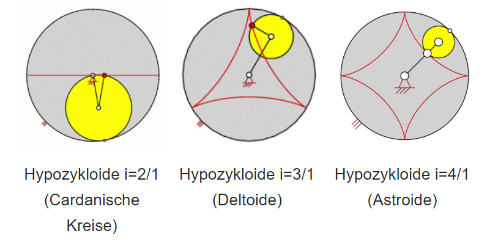
Spezielle Hypozykloiden:
- Für i = 2 (Cardanische Kreise) ergibt sich eine geradlinige Hypozykloide, deren sämtliche Punkte auf einem Durchmesser liegen.
- Für i = 3 ergibt sich eine Deltoide (Hypozykloide mit 3 Spitzen)
- Für i = 4 ergibt sich eine Astroide: das Karo, wie man es von Spielkarten kennt.
