Área da Superfície do Trapézio

Autor:Romulo Soares, felipeph, Jorge Cássio

Nesta atividade você irá investigar uma figura plana bastante conhecida, o Trapézio.

Um trapézio é um quadrilátero convexo que possui somente dois lados paralelos entre si. Chamamos esses lados paralelos de bases (maior e menor) do trapézio. Antes de pensarmos na fórmula, tente preencher a superfície do trapézio a seguir, unindo as peças corretamente.

Construção 1: Siga as instruções para preencher a superfície do trapézio, a partir de outras figuras planas. Tente realizar mais de uma combinação, modificando a figura menor para gerar novos trapézios.

Quantos trapézios diferentes você conseguiu montar?

Você concorda que a área da superfície do trapézio obtido é igual à soma das áreas das peças usadas para montá-lo? Por quê?

Você acha que da mesma forma que usou outras figuras planas para construir o trapézio, seria possível "recortar um trapézio" em diferentes peças e montar outra figura plana conhecida com essas peças? Qual figura você montaria? As áreas do trapézio e da sua figura seriam iguais ou diferentes? Explique seu raciocínio.

Agora que já fizemos algumas observações gerais, vamos verificar de uma forma simples porque a área da superfície de um trapézio é determinada pela expressão:

ou, de forma resumida,

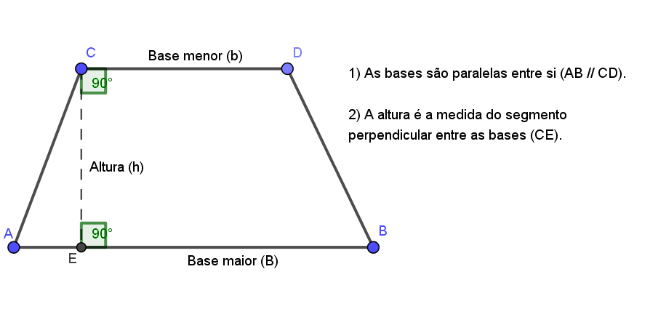
. Observe na imagem os elementos que aparecem na expressão acima (Base maior, Base menor e Altura), e algumas de suas propriedades.

Você certamente já estudou sobre retângulos e triângulos, e sabe que a área da superfície de um retângulo é obtida pela expressão e da superfície de um triângulo pela expressão . Na sua opinião, a fórmula para o cálculo da superfície do trapézio é mais parecida com a fórmula do retângulo ou do triângulo?

Assinale a sua resposta aqui

A
Triângulo
B
Retângulo

Verifique minha resposta (3)

Construção 2: Utilizando a ideia anterior de recortar o trapézio, observe o que acontece ao manipular a próxima construção. Movimente o controle giro para alterar a figura.

Quando o giro está em 0°, qual figura obtemos?

E quando o giro está em 180°, qual a figura obtida?

Note que a área de ambas as figuras é a mesma, apesar de serem figuras diferentes, pois são formadas pelas mesmas "peças" colocadas em posições diferentes. Marque a caixa Mostrar corte para visualizar os detalhes do recorte feito no trapézio. Reconhecendo que as áreas são iguais podemos deduzir a fórmula da área do trapézio utilizando o triângulo obtido ao girar a peça em 180°. Basta observarmos que a base deste triângulo é a soma das duas bases do trapézio.

Assim a área do triângulo (e consequentemente do trapézio) será:

Vamos fixar esta ideia. Na construção abaixo, marque as caixas Mostrar corte e Mostrar bases e altura, em seguida movimente a barra de giro.

Note que a altura é a mesma para o trapézio e para o triângulo, ela não se altera. Veja também, que ao formarmos o triângulo ADF (coloque o giro em 180°), a Base Menor do trapézio ABED se "desloca" para baixo, ficando alinhada com a Base Maior e formando com ela a base do triângulo ADF, como explicado anteriormente. Por isso temos que: Área de ABED = Área de ADF =

Área da Superfície do Trapézio

Nesta atividade você irá investigar uma figura plana bastante conhecida, o Trapézio.

Construção 1: Siga as instruções para preencher a superfície do trapézio, a partir de outras figuras planas. Tente realizar mais de uma combinação, modificando a figura menor para gerar novos trapézios.

Construção 2: Utilizando a ideia anterior de recortar o trapézio, observe o que acontece ao manipular a próxima construção. Movimente o controle giro para alterar a figura.

Novos Materiais

Descobrir recursos

Explorar Tópicos