Surface Area of a Sphere
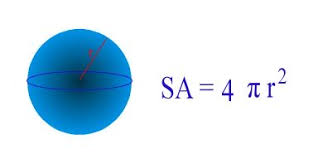
The surface area of a sphere of radius r is:
Archimedes first derived this formula from the fact that the projection to the lateral surface of a circumscribed cylinder is area-preserving.Another approach to obtaining the formula comes from the fact that it equals the derivative of the formula for the volume with respect to r because the total volume inside a sphere of radius r can be thought of as the summation of the surface area of an infinite number of spherical shells of infinitesimal thickness concentrically stacked inside one another from radius 0 to radius r. At infinitesimal thickness the discrepancy between the inner and outer surface area of any given shell is infinitesimal, and the elemental volume at radius r is simply the product of the surface area at radius r and the infinitesimal thickness. At any given radius r,the incremental volume (δV) equals the product of the surface area at radius r (A(r)) and the thickness of a shell (δr):
The total volume is the summation of all shell volumes:
In the limit as δr approaches zero[8] this equation becomes:
Substitute V:
Differentiating both sides of this equation with respect to r yields A as a function of r:{\displaystyle 4\pi r^{2}=A(r).}
This is generally abbreviated as:{\displaystyle A=4\pi r^{2},}
where r is now considered to be the fixed radius of the sphere. Alternatively, the area element on the sphere is given in spherical coordinates by dA = r2 sin θ dθ dφ. In Cartesian coordinates, the area element is:
The total area can thus be obtained by integration:
The sphere has the smallest surface area of all surfaces that enclose a given volume, and it encloses the largest volume among all closed surfaces with a given surface area. The sphere, therefore, appears in nature: for example, bubbles and small water drops are roughly spherical because the surface tension locally minimizes surface area. The surface area relative to the mass of a ball is called the specific surface area and can be expressed from the above-stated equations as:
where ρ is the density
Archimedes first derived this formula from the fact that the projection to the lateral surface of a circumscribed cylinder is area-preserving.Another approach to obtaining the formula comes from the fact that it equals the derivative of the formula for the volume with respect to r because the total volume inside a sphere of radius r can be thought of as the summation of the surface area of an infinite number of spherical shells of infinitesimal thickness concentrically stacked inside one another from radius 0 to radius r. At infinitesimal thickness the discrepancy between the inner and outer surface area of any given shell is infinitesimal, and the elemental volume at radius r is simply the product of the surface area at radius r and the infinitesimal thickness. At any given radius r,the incremental volume (δV) equals the product of the surface area at radius r (A(r)) and the thickness of a shell (δr):
The total volume is the summation of all shell volumes:
In the limit as δr approaches zero[8] this equation becomes:
Substitute V:
Differentiating both sides of this equation with respect to r yields A as a function of r:{\displaystyle 4\pi r^{2}=A(r).}This is generally abbreviated as:{\displaystyle A=4\pi r^{2},}where r is now considered to be the fixed radius of the sphere. Alternatively, the area element on the sphere is given in spherical coordinates by dA = r2 sin θ dθ dφ. In Cartesian coordinates, the area element is:
The total area can thus be obtained by integration:
The sphere has the smallest surface area of all surfaces that enclose a given volume, and it encloses the largest volume among all closed surfaces with a given surface area. The sphere, therefore, appears in nature: for example, bubbles and small water drops are roughly spherical because the surface tension locally minimizes surface area. The surface area relative to the mass of a ball is called the specific surface area and can be expressed from the above-stated equations as:
where ρ is the density