Beugungsexplorer hinter dem breiten Spalt
Simulation der Fresnel-Beugung am breiten Spalt unter Verwendung von Integralen, die mit zwei Methoden berechnet wurden: Fresnel-Näherung und Huygens-Fresnel-Prinzip. (en.: Simulation of Fresnel diffraction through a wide slit using integrals calculated by two methods: Fresnel approximation and Huygens-Fresnel principle.)
Die Besonderheiten von breiten und schmalen Spalten sind im Artikel beschrieben. Als charakteristisches Merkmal für diese Breite nehmen wir das Verhältnis der Breite des Spaltes b zur Wellenlänge λ: b / λ. In diesem Applet ist [b/λ]=300, d.h. in Spaltnähe: im Bereich der geometrischen Optik, ist die Anzahl der Peaks der Intensitätsverteilung in der Ebene parallel zur Spaltebene gleich diesem Verhältnis. Die charakteristischen Beugungsstreifen in der Nähe der Spaltkanten sind Merkmale der Kantenbeugung.
Die Interpretation der erhaltenen Bilder ist im Applet zu finden.
☞
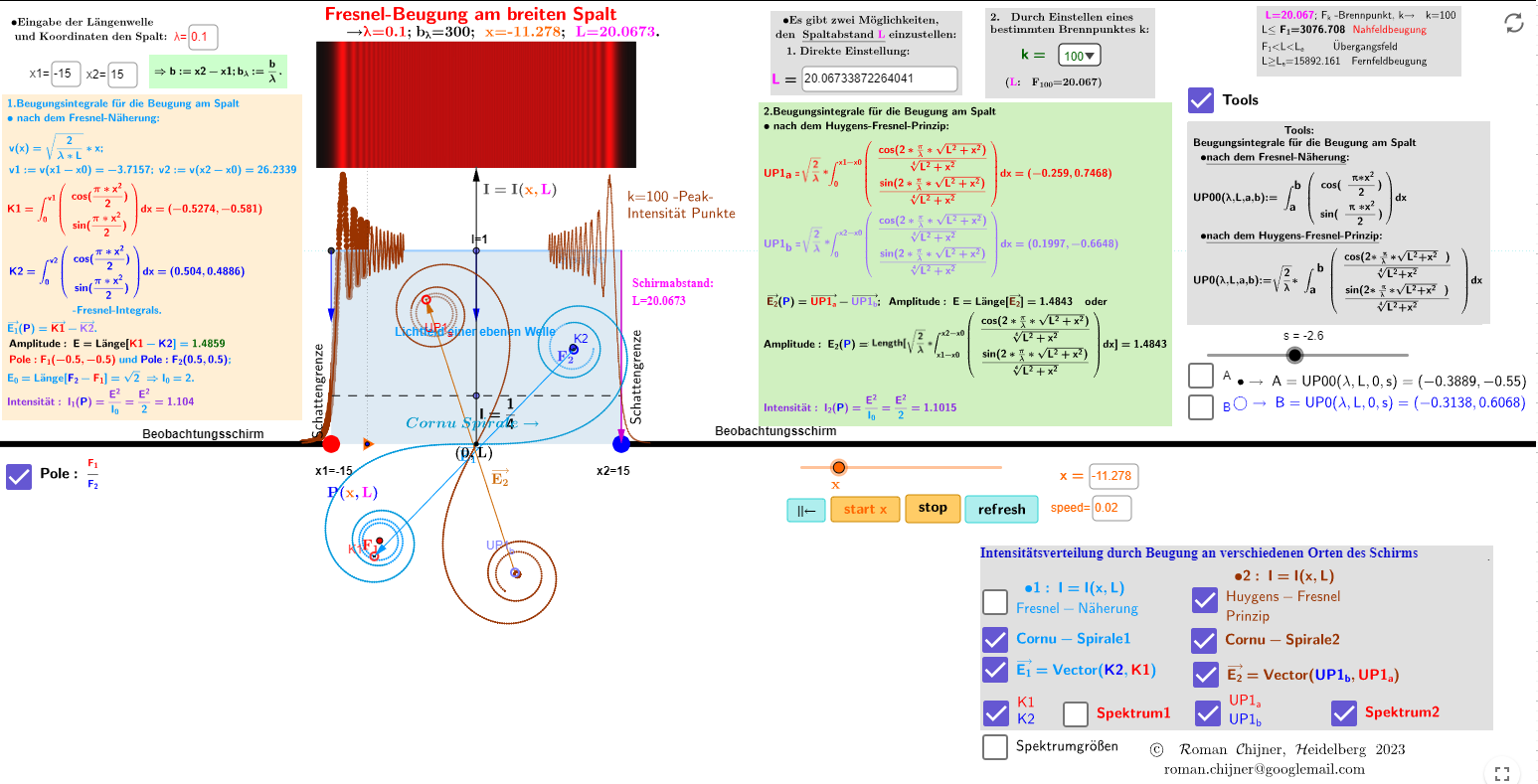
![[size=85] Zu beachten sind: Für den Fall, dass die Spaltbreite (b:=x2-x1) um ein Vielfaches größer ist als die Länge (λ) der einfallenden ebenen Welle: b[sub]λ[/sub]>>1, sind die Ergebnisse der Beugungsintegrale der Fresnel-Näherung und die nach Huygens-Fresnel-Prinzip liegen nahe beieinander. In einigen Fällen in der Nähe der Spaltfläche funktioniert die Fresnel-Näherung jedoch nicht (siehe Abb. 4 in [url=https://www.geogebra.org/m/pbwwfyra]Applet[/url]).[/size]](https://www.geogebra.org/resource/ypnkr4ex/TB1H4xZHwvF7LYHS/material-ypnkr4ex.png)