L6.4 - Distances and Circles
Learning Intentions and Success Criteria
- Generalize (using words and other representations) the process of repeated distance calculations to derive an equation for a circle in the coordinate plane.
- Derive an equation for a circle in the coordinate plane.
4.1: Going the Distance
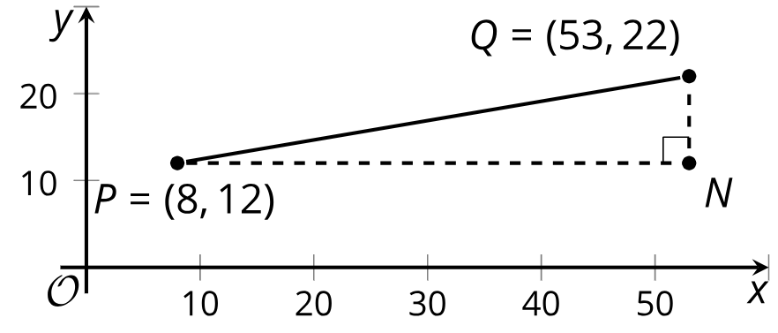
Andre says, “I know that I can find the distance between two points in the plane by drawing in a right triangle and using the Pythagorean Theorem. But I’m not sure how to find the lengths of the legs of the triangle when I can’t just count the squares on the graph.” Explain to Andre how he can find the lengths of the legs in the triangle in the image. Then, calculate the distance between points P and Q.
4.2: Circling the Problem
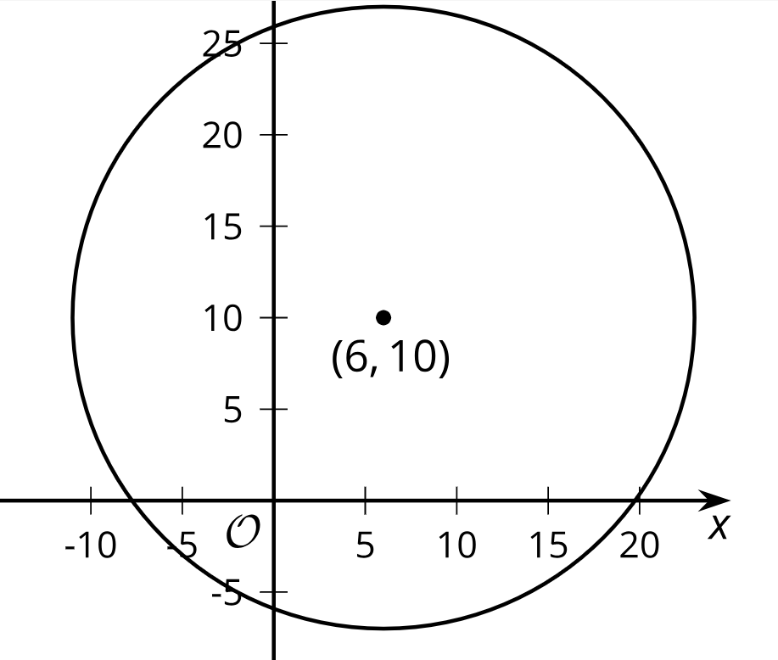
The image shows a circle with center (6,10) and radius 17 units. 1. The point (14,25) looks like it might be on the circle. Verify if it really is on the circle. Explain or show your reasoning.
2. The point (22,3) looks like it might be on the circle. Verify if it really is on the circle. Explain or show your reasoning.
3. In general, how can you check if a particular point (x, y) is on the circle?
4.2: Circling the Problem
4.3: Building an Equation for a Circle
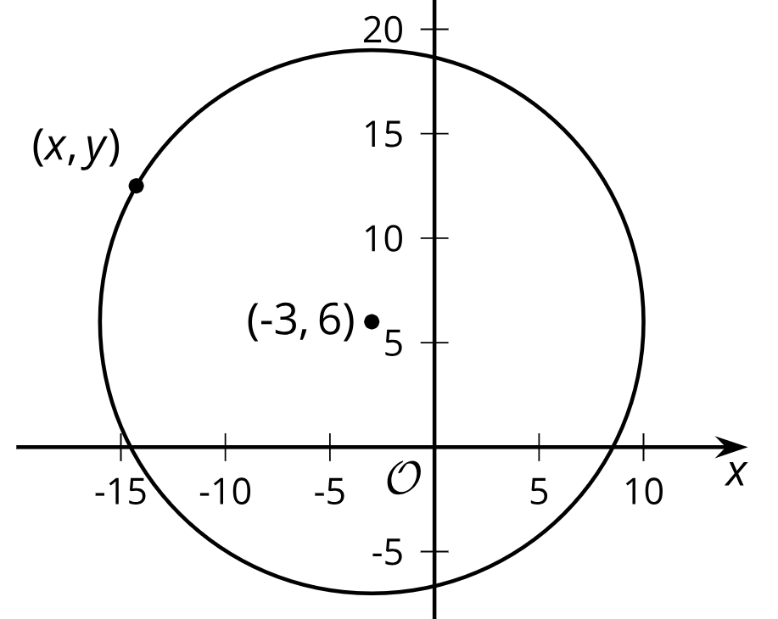
The image shows a circle with center (-3, 6) and radius 13 units. 1. Write an equation that would allow you to test whether a particular point (x, y) is on the circle.
2. Use your equation to test whether (9, 1) is on the circle.
3. Suppose you have a circle with center (h, k) and radius r. Write an equation that would allow you to test whether a particular point (x, y) is on the circle.

Learning Intentions and Success Criteria
- Generalize (using words and other representations) the process of repeated distance calculations to derive an equation for a circle in the coordinate plane.
- Derive an equation for a circle in the coordinate plane.
Cool-Down: Writing Circle Equations
1.
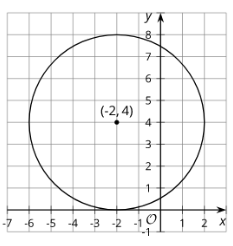
1.
2.