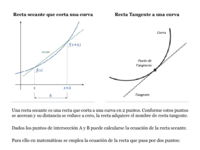
Introducción al concepto geométrico de Derivada
El siguiente recurso pretende consolidar la comprensión del concepto de Derivada.
A continuación se realizan algunas preguntas relacionadas con el concepto de Derivada:
Si se mueve el deslizador "h", se mueve:
¿En que valor de "h" la recta secante se convierte en recta tangente?
Por lo anterior se concluye que si la distancia "h" se acerca a cero la recta secante se convierte en una recta:
A continuación se presentan algunos conceptos que ayudaran a validar las respuestas a las preguntas anteriores.
Recta Secante
Las coordenadas del punto A, del recurso planteado, son:
Las coordenadas del punto B, del recurso planteado son:
Con base a las coordenadas del punto A y B, del recurso planteado hallar la pendiente de la recta, teniendo en cuenta la ecuación de la pendiente planteada anteriormente, es decir:
null
Con base a las coordenadas del punto A y B, del recurso planteado hallar la pendiente de la recta, teniendo en cuenta la ecuación de la pendiente planteada anteriormente, es decir: Pendiente =
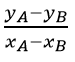
Contrastar la pendiente hallada y compararla con la definición del concepto de derivada planteada a continuación, para establer conclusiones.
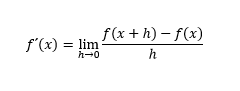
Socializa las conclusiones con tus compañeros y validalas con el profesor.
Muchas gracias por su compromiso y dedicación en esta actividad!