Hodnost matice
Hodnost matice je maximální počet lineárně nezávislých řádků.
Řádky považujeme za aritmetické vektory .
Poznámka: Ekvivalentně bychom mohli definovat hodnost matice pomocí sloupcových vektorů.
Můžeme používat tyto úpravy bez toho, aniž bychom změnili hodnost matice:
- Prohodit libovolné dva řádky.
- Vynásobit řádek libovolným nenulovým výrazem.
- Přičíst jeden řádek ke druhému.
- Všechny předchozí úpravy lze použít i na sloupce
Ekvivalentní úpravy matice *
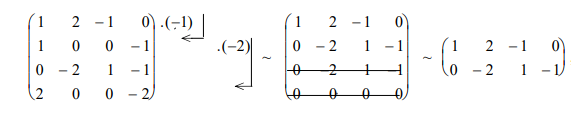
Matici můžeme v GeoGebře zadávat tabulkou. Menu Zobrazit>>Tabulka otevře prostředí podobné Excelu. Tabulku hodnot označíme a nástrojem Matice
exportujeme do algebraického okna.
Druhým (rychlejším) způsobem je, zadat matici jako seznam řádků ve složených závorkách. Každý řádek je ohraničen složenými závorkami, prvky jsou odděleny čárkou. Např:
exportujeme do algebraického okna.
Druhým (rychlejším) způsobem je, zadat matici jako seznam řádků ve složených závorkách. Každý řádek je ohraničen složenými závorkami, prvky jsou odděleny čárkou. Např:
A={{1,2}, {3,4}}
V appletu níže je zadána matice A z předchozího příkladu, ekvivalentní matici elimA získáme použitím příkazu SchodovityTvar(A).
Matice elimA má hodnost 2, ale poskytuje jinou bázi vektorového podprostoru než rozepsané ekvivalentní úpravy * výše.
Vektory (1, 2, -1, 0), (1, 0, 0, -1), (0, -2, 1,-1) a (2, 0, 0, 2) jsou lineárně závislé, generují jen vektorový prostor dimenze 2. Bazí tohoto podprostoru může být například dvojice vektorů (1, 2,-1, 0), (0,-2,1,-1) nebo (1, 0, 0, -1), (0, 1, -0.5, 0.5).
Úloha
Mezi danými vektory a = (1, 0, 0), b = (0, 1, 1), c = (1, 1, 1), d = (1, 2, 2) najděte maximální počet lineárně nezávislých vektorů. Určete dimenzi vektorového prostoru, který generují.
Příklad (Matematika I, str. 60)
V appletu výše je vyřešena úloha 12 a) pomocí Gaussovy eliminace matice M.
Mel = SchodovityTvar(M)
Hodnost matice Mel je dva, jako generátory stačí vybrat jakékoliv dva lineárně nezávislé řádky. Doplníme-li první dva vektory (2, 1, -1, 4) a (-1, 3, 0, -1) vektory (0, 0, 1, 0) a (0, 0, 0, 1) získáme bázi celého R4.Seznam užitečných příkazů:
Hodnost(A)
Determinant(A)
SchodovityTvar(A)
Invertovat(A)
Transponovat(A)
Podrobnější vysvětlení na serveru Matematika.cz, kapitola Hodnost matice.