Graphical representation of the complex amplitude of a single slit diffraction/Grafische Darstellung der komplexen Amplitude einer Einzelspaltbeugung (GIF-Animation).
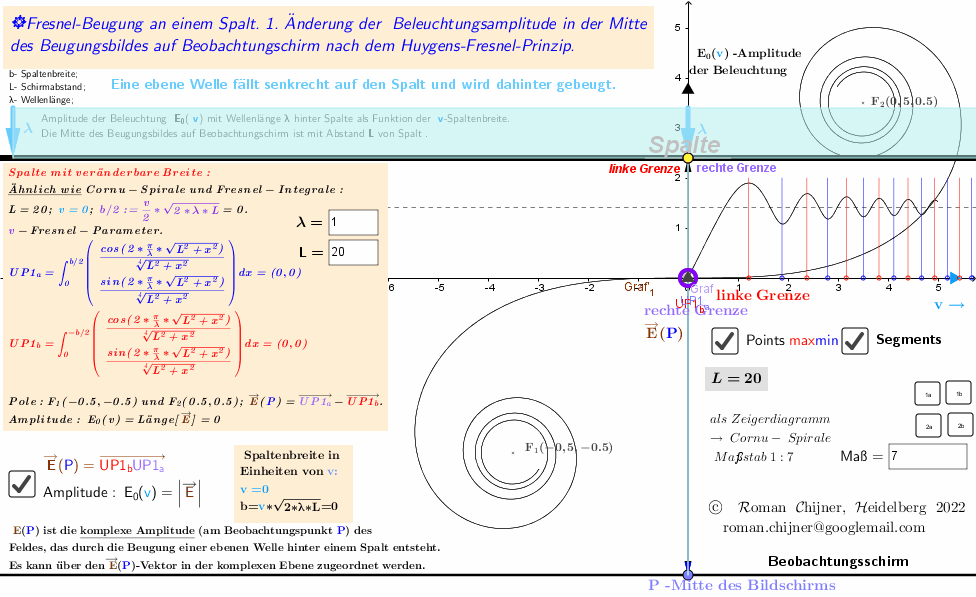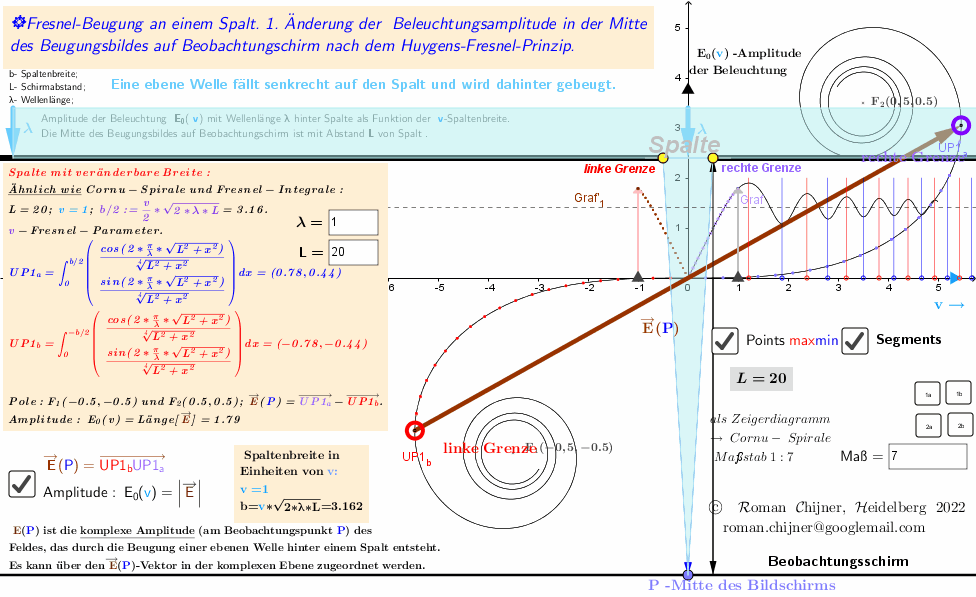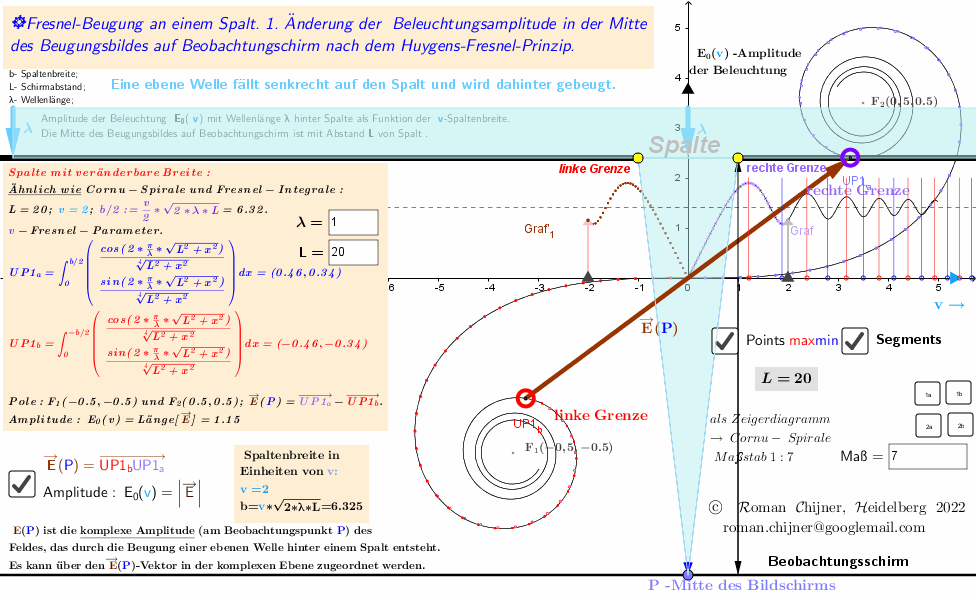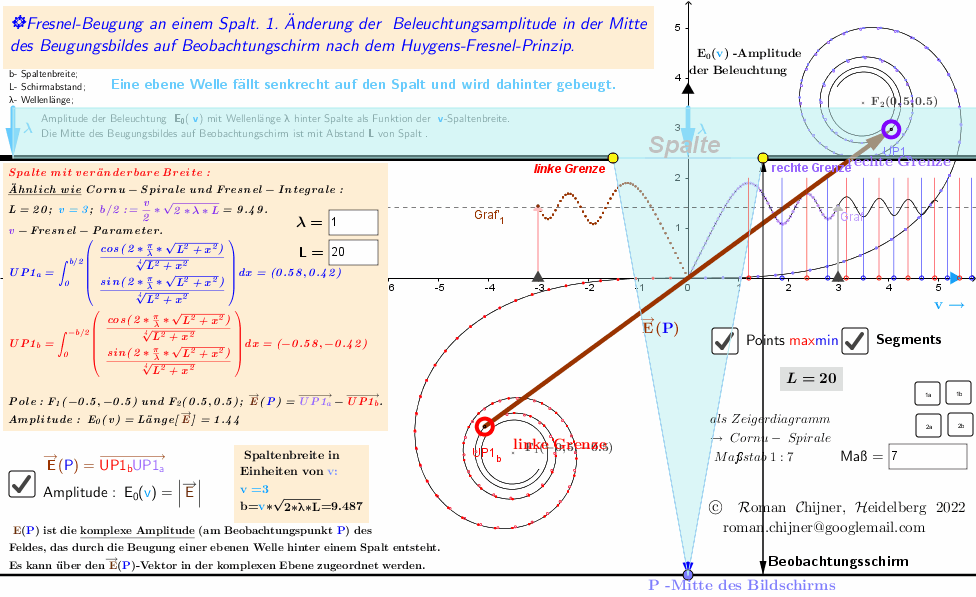
Das Applet visualisiert gleichzeitig das Verhalten der komplexen Amplitude (resultierender Schwingungsvektor auf einem Vektordiagramm -Cornu-Spirale) in der Mitte des Bildschirms des Beugungsmusters hinter dem Spalt und das Amplitudenänderungsdiagramm dieses Vektors in Abhängigkeit von der Spaltenbreite. Applet ist in https://www.geogebra.org/m/t2t3mtse.
Bei der Beschreibung von Nahfeldbeugungsphänomenen in der Fresnel-Näherung wird die komplexe Amplitude des Feldes am Beobachtungspunkt durch das Integral berechnet (nach Real- und Imaginärteil aufgetrennt : C+ ί *S) und als Fresnel-Integral bezeichnet. Bei der numerischen Berechnung des Beugungsintegrals nach dem Huygens-Fresnel-Prinzip ergeben sich weitere Integrale, die ich in dieser Rechnung "verallgemeinerte" Fresnel-Integrale nenne (siehe Applet).
 .
Die resultierende parametrische Kurve (C, S) wird auch als "verallgemeinerte" Cornu-Spirale bezeichnet.
.
Die resultierende parametrische Kurve (C, S) wird auch als "verallgemeinerte" Cornu-Spirale bezeichnet.