Números Complejos
Los Números Complejos C
Los números complejos son combinaciones de números reales y números imaginarios.
En otras palabras, los números complejos son números que tienen una parte real y una parte imaginaria.
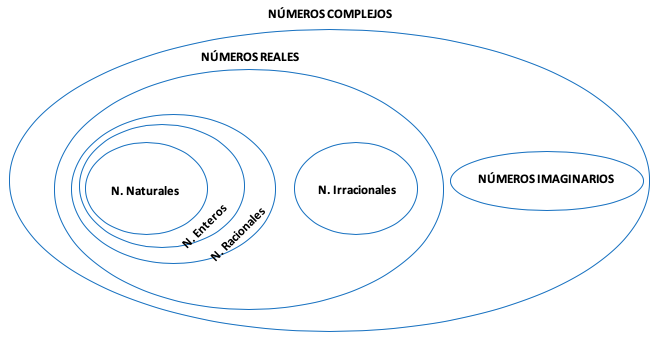
Números reales e imaginarios
Los números reales son cualquier número que corresponda a un punto en la recta real y pueden clasificarse en números naturales, enteros, racionales e irracionales.
Cualquier número real está comprendido entre menos infinito y más infinito y podemos representarlo en la recta real.
Los números imaginarios forman parte del conjunto de los números complejos y son el producto de un número real por la unidad imaginaria i.
Se utiliza la i para denotar la unidad imaginaria.
Ejemplo de números complejos
4 + 8i
4 número real
8i numero imaginario
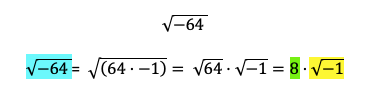
La raíz cuadrada de -1 es conocida como la unidad imaginaria.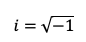
Unidad imaginaria
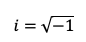Unidad imaginaria Un número complejo z en forma binómica se representará de la forma a+bi y su afijo o forma de par ordenado es (a,b).
Complejos opuestos
Dos complejos son opuestos si la suma de ambos es igual a cero. Esto quiere decir que el opuesto de un complejo se obtiene al cambiar los signos al número complejo dado.
Si Z= a+bi su opuesto es -Z=-a-bi
Complejos conjugados
Dado el complejo Z=a+bi el conjugado es Z=a-bi, el conjugado es el mismo número complejo con el signo de la parte imaginaria cambiada.
Completa la tabla
Selecciona la respuesta correcta
1. Forma parte del conjunto de los números complejos y son el producto de un número real por la unidad imaginaria:
2. La unidad imaginaria se representa por:
3. Es un número complejo
¿Qué son los números complejos?
Representación grafica de números complejos
Para representar gráficamente un número complejo, debemos dibujarlos en el plano complejo. Éste está formado por un eje real y un eje imaginario. Sobre el eje real representaremos la parte real del número complejo, mientras que en el eje imaginario representaremos la parte imaginaria.
Esta formado por cuatro cuadrantes.
Te invito jugar y aprender: ubicando los ejes y los cuadrantes en el plano Gaussiano.
Los números complejos se representan en forma gráfica, en el plano Gaussiano, donde la parte real se coloca en el eje horizontal y la parte imaginaria en el eje vertical.
Z=a+bi en su forma binómica, la forma gráfica es: (a,b).
Ubica los diferentes puntos que están en el plano en los diferentes cuadrantes y en los ejes; copia en el cuaderno los puntos obtenidos en cada cuadrante.
Módulo de un número complejo
En matemáticas, el módulo de un número complejo es el número real positivo que mide su tamaño y generaliza el valor absoluto de un número real. Esta noción es particularmente útil para definir una distancia en el plano complejo. El módulo de un número complejo z se denota como |z|.
Y se calcula con /Z/=
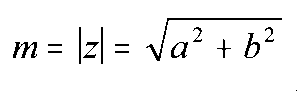
Ejemplos
Ubica 5 puntos diferentes de A, B y C en el plano y obtén su módulo.
Mueve "a" para obtener diferentes números reales y "b" para la parte imaginaria. Observará su conjugado, opuesto y su módulo en cada movimiento. Toma un punto y explicara su procedimiento.
Operaciones de números complejos en forma binómica
* Suma de números complejos
La suma de dos números complejos es otro número complejo cuya parte real es la suma de las partes reales y cuya parte imaginaria que es la suma de las partes imaginarias.
(a+bi) +(c+di)=(a+c) + (b+d)i
*Resta de números complejos
Para restar dos números complejos, reste la parte real de la parte real y la parte imaginaria de la parte imaginaria.
(a+bi) - (c+di)= (a+bi) + (-c-di)= (a-c) + (b-d)i
*Multiplicación de números complejos
El producto de los números complejos se realiza aplicando la propiedad distributiva del producto respecto de la suma y teniendo en cuenta que i2= −1.
(a + bi) · (c + di) = (ac − bd) + (ad + bc)i
*División de números complejos
Para dividir dos complejos se multiplica el numerador y el denominador por el conjugado del denominador, así el denominador pasará a ser un número real. Finalmente se separan la parte real y la parte imaginaria.