Contour
Quadratische Funktionen 2023
Kaum eine Parabel, die in der Technik oder Natur vorkommt, hat die Form einer Normalparabel.
https://upload.wikimedia.org/wikipedia/commons/thumb/5/53/Duisburg_Bruecke_der_Solidaritaet.jpg/800px-Duisburg_Bruecke_der_Solidaritaet.jpg https://upload.wikimedia.org/wikipedia/commons/c/cd/Orange_Bridge._Can%27t_Miss_It-edit.jpg https://cdn.pixabay.com/photo/2016/07/16/16/12/tyne-bridges-1522241_960_720.jpg
Wir werden untersuchen, wie die Funktionsgleichung der Normalparabel angepasst werden muss, um z.B. den Verlauf von Brücken durch eine Parabel zu beschreiben.
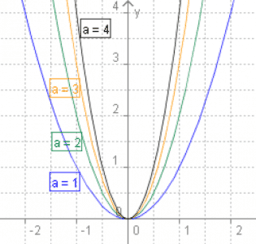
Table des matières
Einführung
Die Normalparabel f(x)=x²
Streckung und Stauchung: f(x) = a*x²
Verschiebungen der Normalparabel
f(x) = x² + e
f(x) = (x - d)²
f(x) = (x - d)² + e
Scheitelpunktform: Quadratische Funktionen der Form f(x) = a*(x - d)² + e
Beschreibung der Eigenschaften einer Quadratischen Funktion
- Öffnungsverhalten einer Parabel
- Streckung und Stauchung der Normalparabel
- Streckung und Stauchung der Normalparabel, a negativ
- Was ist eine Nullstelle?
- Anzahl der Nullstellen einer Qudratischen Funktionen
- Übungen: Scheitelpunkte anhand von Parabelgleichungen bestimmen
- Übungen: Scheitelpunkt, Form und Lage einer Parabel anhand Scheitelpunktform bestimmen
- Übungen: Parabeln ihre Parabelgleichung zuordnen
- Übungen: Nullstellen quadratischer Funktionen in Scheitelpunktform bestimmen
Parabelgleichung an Brücke anpassen
Von der Scheitelpunktsform zur Normalform (allgemeinen Form)
- Von der Scheitelpunktform zur Normalform
- Scheitelpunktform quadratischer Funktionen
- Von der Scheitelform der Parabel in die Normalform
- Parabel - Scheitelform in Allgemeine Form, einfach (9I.7 | 10II.4)
- Parabel - Scheitelform in Allgemeine Form (9I.7 | 10II.4)
- Übungen: Binomische Formeln ausmultiplizieren
Von der Allgemeinen Form (Normalform) in die Scheitelpunktform
Funktionentrainer
Modellierungsaufgaben (Zusatz)
Gemischtes (Zusatz)