M1 L Didaktische Hinweise

Grobstruktur der Sequenz und Kapitel dieses Buches
Kapitel I: Lokale Änderungsrate (numerisch)
Erarbeitung der Grundvorstellung Lokale Änderungsrate im Anwendungskontext schnellstes Landtier Gepard durch den Grenzübergang von mittlerer Geschwindigkeit zu momentaner Geschwindigkeit.
Verbale Definition auf dieser Basis und Ausweitung der Begriffe Bestand, absolute Änderung und mittlere sowie lokale Änderungsrate auf andere Kontexte.
Optional auch eine formal algebraische Betrachtung und Definition der Ableitung (und der Differenzierbarkeit) mit dem Übergang vom Differenzenquotient (der mittleren Geschwindigkeit) zum Differentialquotient (der Momentangeschwindigkeit) (s. Abschnitt optional: Weg(Zeit)-Funktion modellieren).
Kapitel II: Tangentensteigung (graphisch)
Erarbeitung der Grundvorstellung Tangentensteigung zunächst im Kontext Gepard.
Explizite Umdeutung der Tangente vom geometrischen hin zu einem analytischen Verständnis.
Formal algebraische Betrachtung und Definition der Ableitung (und der Differenzierbarkeit) mit dem Übergang von dem Differenzenquotienten aus der Tangentensteigung zum Differentialquotient (s. Abschnitt 3. Schritt: Tangentensteigung als Grenzwert).
Kapitel III: Übergang zur Ableitungsfunktion
Übergang von der Ableitung an einer Stelle zu der Ableitung als Funktion durch "graphisches Ableiten" in GeoGebra-MMS.
Hinweis zu den Begriffen
Die Begrifflichkeiten, die im Kontext Gepard eingeführt werden, stellen eine wichtige Grundlage für die gesamte Differentialrechnung dar.
Insbesondere die Unterscheidung von Bestand und Änderung und damit verbunden Bestandsfunktion und Ableitungsfunktion unterstützen später die Begriffsbildung beim Integral.
Verständnis des Ableitungsbegriffs
Beim Einstieg in die Differenzialrechnung wird häufig ein graphischer Zugang über die Tangente an einen Funktionsgraph genutzt. Diese Herangehensweise hat zwei entscheidende Nachteile:
- die Hürde der Umdeutung des bisher geometrisch mithilfe des Kreises geprägten Begriffs Tangente auf Funktionsgraphen erschwert den Aufbau einer Vorstellung zum Begriff Ableitung
- die zentrale Grundvorstellung (s.u.) der Ableitung als Beschreibung des Änderungsverhaltens eines funktionalen Zusammenhangs wird durch die rein graphische Betrachtung nicht deutlich.
Grundvorstellungen zur Ableitung
Wie für die zentralen Begriffe der Mittelstufe sind auch für die Ableitung sogenannte Grundvorstellungen (GV) beschrieben, die abstrakte Begriffe anschaulich repräsentieren und Verbindungen zwischen Mathematik und Anwendungssituationen ermöglichen.
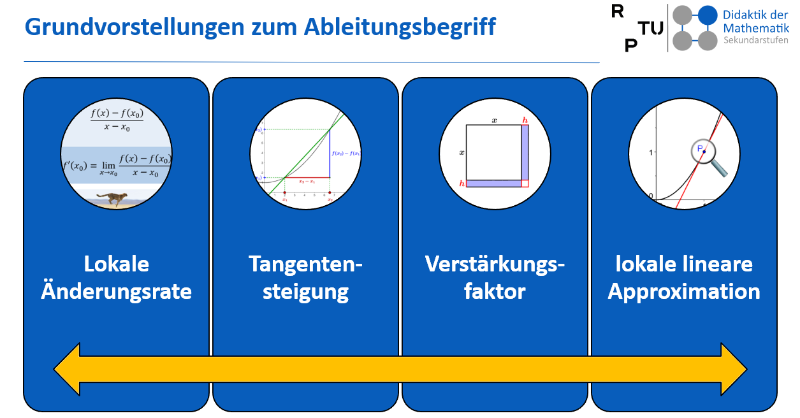
Nachfolgende Abbildung gibt einen Überblick über die beschriebenen Grundvorstellungen zur Ableitung, Details zu den einzelnen Grundvorstellungen finden sich u.a. bei Roth und Siller (2016).
Fokus dieser Sequenz sind die beiden GV lokale Änderungsrate und Tangentensteigung.
Zu den beiden anderen GV finden sich Materialien im Kapitel Anregungen für den weiteren Unterricht.
GeoGebra-Applet, GeoGebra-Aktivität und GeoGebra-MMS
GeoGebra ist in der folgenden Sequenz in verschiedenen Einsatzszenarien eingebunden, die unterschiedlich benannt sind:
GeoGebra-Applet bezeichnet eine vorkonfigurierte GeoGebra-Datei, wie sie in einer Vielzahl auf der Webseite von GeoGebra unter Materialien zu finden ist.
GeoGebra-Aktivitäten sind ebenfalls online unter Materialien zu finden, beinhalten aber neben einem GeoGebra-Applet weitere Elemente wie Aufgaben, Texte, Abbildungen oder weitere GeoGebra-Applets.
GeoGebra-MMS bezeichnet hier die Nutzung der GeoGebra-Oberfläche (Rechner Suite, Classic mit/ohne Prüfungsmodus) OHNE vorkonfigurierte Bestandteile.
Die unterschiedlichen Perspektiven für deren Einsatz im Unterricht wird im Abschnitt Einsatz von GeoGebra im Unterricht genauer beschrieben.
Link zu den Fortbildungsmaterialien von Modul 1
Link zur Präsentation (folgt)