Spline cúbica con frontera sujeta
La propiedad e), establece que se cumple solo una de las siguientes condiciones de frontera
- (frontera libre o frontera natural, spline cúbica natural)
- y (spline cúbica con frontera sujeta)
La primera condición de frontera la hemos visto en el capítulo anterior. La segunda condición resulta de gran utilidad ya que son las primeras derivadas y las que establecen los valores respectivos de y especificados por el usuario. Por lo cual se tiene el control de la pendiente al principio y al final del spline.
Para el extremo izquierdo, si , implica que
Por la propiedad d) de las propiedades de la spline cúbica y dado que tenemos que
tomando en cuenta que y , la diferencia se puede expresar como
ahora, de la construcción de trazadores cúbicos para sabemos que y , entonces
sabemos también que para , , entonces
operando algebraicamente, nos queda
(9)
Para el extremo derecho, si , entonces
sustituyendo y en la ecuación anterior, tenemos
operando algebraicamente, nos queda
(10)
Así, de (9) y (10),la matriz definida en el capítulo anterior queda de la siguiente manera (Sauer, 2012)
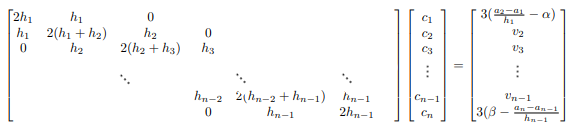
al ser una matriz diagonal estrictamente dominante, tiene solución única, es decir, la spline cúbica con frontera sujeta es única y su demostración es análoga a la unicidad de la spline cúbica natural.