Die Erkundung des Skalarproduktes - nach Daniel Frohn
1. Annäherung an das Skalarprodukt mittels Satz des Pythagoras
Kreuzen Sie zur Kontrolle Ihrer Lösungen an, welche der Vektoren orthogonal zueinander sind.
Sie können den Lösungweg hier notieren. DANACH können Sie das Rechteck verschieben, um die Lösung zu kontrollieren.
Mögliche Bemerkung der Lehrperson an dieser Stelle:
Es wurde nun eine Bedingung für die Orthogonalität von Vektoren gefunden.
Den Term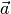 
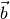= a1b1 + a2b2 + a3b3 definieren wir als Skalarprodukt von zwei Vektoren 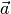und .
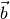Bevor dieses allgemein hergeleitet wird, sollt ihr nun die Eigenschaften des Skalarproduktes untersuchen.
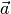
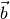= a1b1 + a2b2 + a3b3 definieren wir als Skalarprodukt von zwei Vektoren 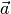und .
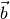Bevor dieses allgemein hergeleitet wird, sollt ihr nun die Eigenschaften des Skalarproduktes untersuchen.2. Eigenschaften des Skalarprodukts
Wenn die Vektoren parallel zueinander sind, dann...
Das Skalarprodukt ändert sich nicht, wenn...
Das Skalarprodukt zweier paralleler Vektoren behält seinen Betrag, aber ändert das Vorzeichen, wenn...
3. Das Skalarprodukt im allgemeinen Fall
Der Skalarprodukt soll nun durch eine Projektion hergeleitet werden. Das bedeutet, dass der zum anderen Vektor senkrechte und parallele Anteil eines Vektors betrachtet wird.
Achtung: Damit die Gleichungen dieser Aufgabe mit der Abbildung übereinstimmen, muss die Projektion von b auf a eingestellt sein. Bei Interesse können die Gleichungen für die Projektion von a auf b analog hergeleitet werden.
Welche geometrische Bedeutung hat das Skalarprodukt von zwei Vektoren?