Die Bogenlänge
Herleitung mit Hilfe von Differentialen
Die Bogenlänge ist die Länge des Funktionsgrafen, wenn man ihn z.B. „gerade ziehen“ würde. Die Herleitung der Bogenlänge ist eine schönes Beispiel, wie man mit Differentialen, wie , tatsächlich rechnen kann:
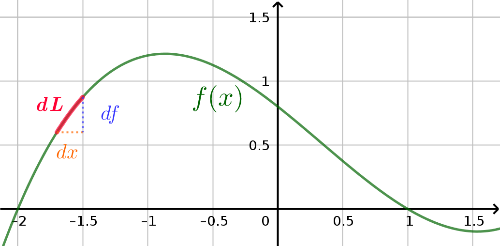
Herleitung der Formel mit Differentialen
Wir betrachten den Funktionsgraphen der Funktion und daraus auch nur ein sehr kleines Stückchen: In der oben stehenden Grafik ist das Stückchen gekennzeichnet. Es ist die Hypothenuse eines winzigen rechtwinkligen Dreieckes mit der Höhe und der Breite .
Differentiale wie , oder stehen immer für sehr kleine Zahlen. Physiker und Techniker schreiben daher eine Ableitung auch als . Der Bruch beschreibt dann genau die Steigung von mit Hilfe dieses kleinen Steigungsdreieckes ( siehe Steigung linearer Funktionen ).
Wir wollen aber die Länge des Funktionsgraphen ausrechnen. Die Länge können wir in einer guten Näherung einfach mit dem Satz des Pythagoras berechnen: oder eben . Denn wenn man das sehr sehr klein wählt, dann ist keine Krümmung zu erkennen, dann ist so gerade wie eine lineare Funktion.
Der Funktionsgraph besteht aus unendlich vielen kleinen 's und wenn man die Länge des Funktionsgraphen berechnen will, muss man die Längen dieser 's alle addieren. In der Mathematik geht so etwas mit einem Integral:
Nun wechselt man die Koordinaten von auf :
Mit Integral sieht das dann so aus:
also
Eine Beispielrechnung
Die oben abgebildete Funktion ist . Wir berechnen die Bogenlänge im Intervall , also von Nullstelle zu Nullstelle. Die Ableitungsfunktion von ist . Damit ist die Bogenlänge:
Da so ein kompliziertes Integral per Hand mit Schulmitteln nicht zu lösen ist, darf diese Rechnung guten Gewissens mit einem CAS gemacht werden.
Ausprobieren:
Hier kann das Intervall zwischen A und B verändert werden, indem die Punkte verschoben werden. Außerdem können Sie eine neue Funktionsgleichung eingeben. Die Bogenlänge wird dabei automatisch berechnet.