5.1. Construindo gráficos de funções
Vamos aprender a construir gráficos de algumas funções.
Começaremos construindo o gráfico da função de lei de formação y = 2x (essa função associa cada número real x ao seu dobro y) Inicialmente montamos uma tabela atribuindo valores a x e calculando, por meio da lei de formação, os valores de y correspondentes. Assim obtemos alguns dos pares ordenados (x, y) dessa função.

em seguida localizamos no plano cartesiano os pontos que representam cada par ordenado. Observe que os pontos estão alinhados. Quanto mais pares ordenados da função representarmos, mais pontos alinhados obteremos.
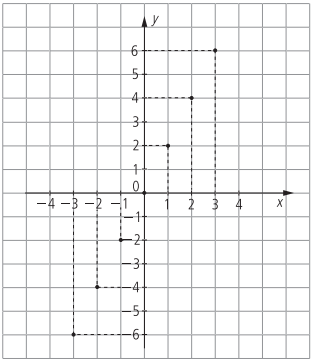
todos os pontos que representam os pares ordenados dessa função formam seu gráfico, que é uma reta.
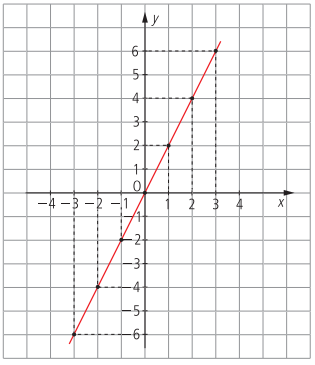
Outro exemplo: Como será o gráfico da função dada por y = -3x + 1?
Montamos uma tabela atribuindo alguns valores para x, calculamos os valores de y por meio da lei de formação da função e representamos no sistema cartesiano os pares ordenados (x, y) obtidos.
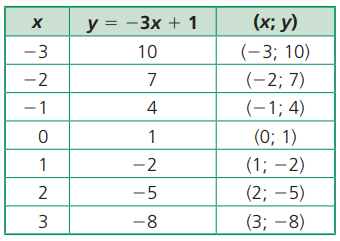
Os pontos obtidos estão alinhados. Quanto mais pares ordenados da função representarmos, mais pontos alinhados obteremos. São infinitos pares ordenados, pois x pode ser qualquer número real. O gráfico dessa função é uma reta.
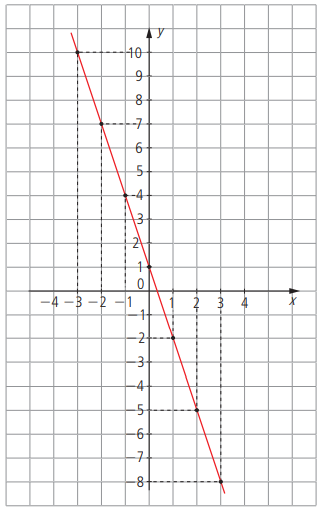

A resposta é não. Vamos montar uma tabela com alguns valores de x e de y para a função dada por y = x² + 2x -1 e representar os pares ordenados (x, y) no sistema cartesiano.
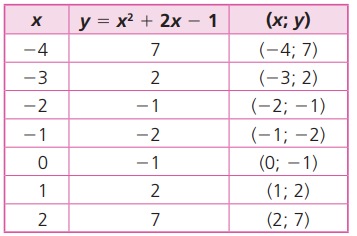
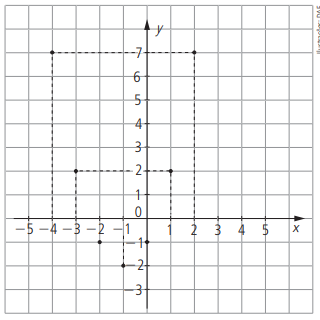
Os pontos não estão alinhados, portanto não determinam uma reta, mas sim uma PARÁBOLA.
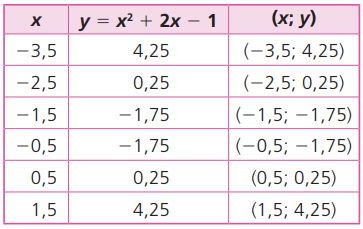
Nessa função, x pode ser qualquer número real. Podemos fazer x = 0,5; x = 124; x = 2,5 etc. Vamos atribuir mais valores a x na tabela, obtendo outros pares ordenados (x; y) da função. Representando mais pontos no sistema cartesiano nos aproximaremos mais
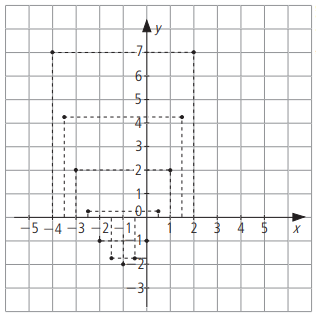
Podemos prosseguir atribuindo valores a x e localizando ainda mais pares ordenados. Todos os pontos que representam os pares ordenados dessa função formam seu gráfico. O gráfico dessa função é uma curva chamada parábola, cuja forma você vê abaixo.
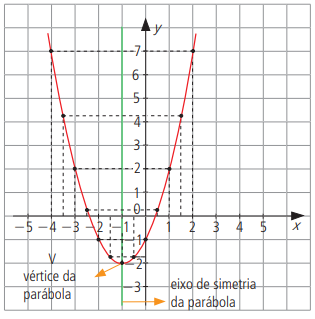
Observe que a parábola possui um eixo de simetria. O ponto da parábola que pertence ao eixo de simetria recebe o nome de vértice (V) da parábola. No gráfico dessa função o vértice tem coordenadas (-1, -2). A parábola que traçamos tem concavidade voltada para cima (ela é “aberta para cima”). No entanto, há funções cujo gráfico é uma parábola com concavidade voltada para baixo.

